Challenge 7 - All the Ones
Challenge 7 is all about number patterns.
Maths teacher Chris Smith and pupils from Grange Academy are here to explain.
The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.
Teacher: This problem is all about number patterns.
If I write out all the whole numbers from 1 to 1000, how many times will I write the digit one? Explain your answer.
Pupil: Try breaking 1000 into smaller groups of numbers and solving these separately.
Pupil: You could try to work out how many times one occurs in the ones tens and hundreds position.
Pupil: Some numbers have a lot more than once.
Pupil: Do your best.
So here's the challenge:
If you were to write out all the whole numbers from 1 to 1000
How many times will I write the digit 1?
Need a hint?
- Can you break 1000 into smaller groups of numbers and solve these separately?
- Could you work out how many times number one occurs in the ones, tens, and hundreds position?
- Remember some numbers have the digit 1 more than once
Solution
Worked out the answer? Here's how you can do it.
Did you work out how many times the digit 1 will occur from 1 to 1000? Let's look how we got our answer.
Chunk the 1000 numbers and check for occurrences of the digit 1.
Between 1 and 9 there's only one 1
Between 10 and 19 that are 11
Remember that 11 itself has two 1's, and between 20 and 99 there are eight 1's.
So there are 20 ones between 1 and 99
There are another 20 between 200 and 299, 300 and 399 and so on, up to 900 and 999
There are more 1's between 100 and 199, because they all start with the 1
Between 100 and 109 that are 11, between 110 and 119 that are 21
Remembering that 111 itself has three 1's
Between 120 and 199 that are another 88
So we have 120 1's between 100 and 199
And don't forget the 1 in 1000
So the total is 20 times 9 add 120, add 1 which equals 301.
Great job if you got all the 1's in this challenge without losing count.
Step 1
Let's chunk the 1000 numbers and check for occurrences of the digit 1.
Between 1 and 9 there is one 1
Between 10 and 19 there are 11 (remembering that 11 itself has two ones).
And between 20 and 99 there are 8 ones.
So between 1 and 99 there are 20 occurrences of the digit 1
Step 2
Now that we know there are 20 ones between 1-99.
This will repeat for most of the groups of 100 numbers.
There are another 20 ones between each of these groups:
200 and 299, 300 and 399, 400 and 499, 500 and 599, 600 and 699, 700 and 799, 800 and 899, 900 and 999
That's another 8 groups of 20 ones.
Step 3
There are more than 20 ones between 100 and 199 because each of these numbers starts with with a one.
Between 100 and 109 there are 11 ones
Between 110 and 119 there are 21 (remembering that 111 itself has three ones).
Between 120 and 199 there are another 88
So we have a total of 120 ones between 100 and 199.
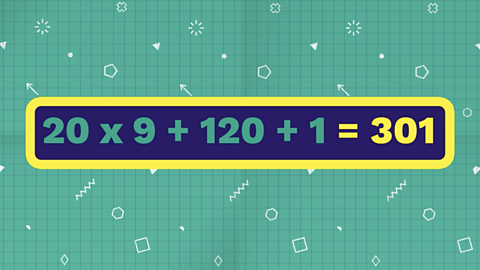
Step 4
Don’t forget the 1 in 1000!
We can now find the total:
20 x 9 + 120 +1 = 301
There are 301 ones between 1 and 1000.
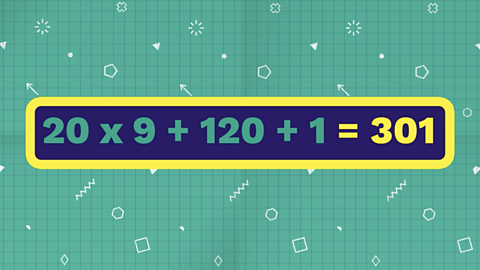
Alternative solution
You can also find the answer by working out the number of ones for each place value:
There are 100 numbers with 1 in the ones (units) position
100 numbers with 1 in the tens position
100 numbers with 1 in the hundreds position
And 1 number with 1 in the thousands position
100 + 100 + 100 + 1 = 301
Which gives us the same total of 301 ones.
Maths Week Scotland 2023. list
Try out all the daily challenges from Maths Week Scotland 2023.
Maths Week Scotland 2022. list
Try out all the daily challenges from Maths Week Scotland 2022.
Maths Week Scotland 2021. list
Want more maths challenges? Here are all the problems from 2021.
More on Maths Week Scotland 2024
Find out more by working through a topic
- count1 of 8
