Key points about how to add, subtract, multiply and divide fractions
- Use the The lowest multiple that is common to two or more numbers. The LCM of 15 and 12 is 60 because it is the lowest value in both of their multiplication tables. Also known as the Least Common Multiple. of the denominators for addition and subtraction.
- A number that is written using a whole number and a fraction, eg 3 ⁴/₅. are converted to A fraction where the numerator is greater than the denominator, eg ⁹⁄₄. for multiplication and division.
- To find a fraction of an amount, divide by the Number written on the bottom of a fraction. The denominator is the number of equal parts, eg for ⅓, the denominator is 3. and multiply by the Number written at the top of a fraction. The numerator is the number of parts used, eg for ⅓, the numerator is 1..
Support your knowledge of this topic by looking at these guides on Lowest Common Multiple and equivalent fractions.
Check your understanding
How to add and subtract fractions and mixed numbers
Look at the examples below on how to add and subtract fractions and mixed numbers.
How to add or subtract fractions:
- When the Number written on the bottom of a fraction. The denominator is the number of equal parts, eg for ⅓, the denominator is 3. are the same:
- Add or subtract the Number written at the top of a fraction. The numerator is the number of parts used, eg for ⅓, the numerator is 1..
- When the denominators are different:
- Find the The lowest multiple that is common to two or more numbers. The LCM of 15 and 12 is 60 because it is the lowest value in both of their multiplication tables. Also known as the Least Common Multiple. of the denominators.
- Rewrite the fractions as A fraction with the same value as another. Each fraction represents the same proportion, eg ½ and ¹⁰⁄₂₀. with the same denominator.
- Add or subtract the numerators.
How to add or subtract mixed numbers:
- Rewrite the A number that is written using a whole number and a fraction, eg 3 ⁴/₅. with equivalent fractions with the same denominator.
- Add or subtract the Integers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, –8, and 10,000 are examples of integers..
- Add or subtract the fractions as above.
How to subtract mixed numbers, when the second fraction is greater than the first fraction:
- Rewrite both fractions as improper fractions, then subtract the fractions.
Sometimes the final answer can be To reduce a fraction to its simplest form, also known as its lowest terms..
If the final answer is an A fraction where the numerator is greater than the denominator, eg ⁹⁄₄., this can also be written as a mixed number.
GCSE exam-style questions
- Complete this calculation:
\(\frac{3}{4}\) – \(\frac{2}{9}\) = \(\frac{19}{36}\)
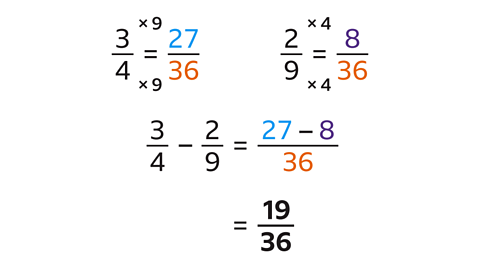
- The denominators are different (4 and 9).
- The lowest common multiple (LCM) of 4 and 9 is the common denominator, 36.
Write the equivalent fractions:
- \(\frac{3}{4}\) is \(\frac{27}{36}\)
- \(\frac{2}{9}\) is \(\frac{8}{36}\)
The subtraction can now be carried out:
- The denominators (36) are the same.
- Subtract the numerators:
- 27 – 8 = 19
- Add these mixed numbers:
\(3\frac{13}{20}\)
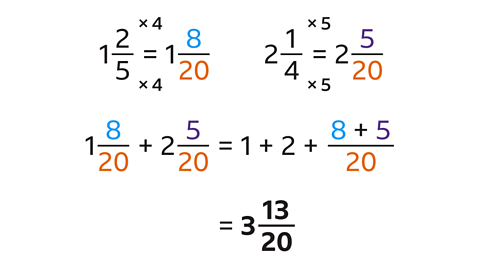
- Rewrite the mixed numbers with equivalent fractions with the same denominator.
- The LCM of 5 and 4 is 20, this is the denominator.
- \(1\frac{2}{5}\) is \(1\frac{8}{20}\)
- \(2\frac{1}{4}\) is \(2\frac{5}{20}\)
- Add the integers: 1 + 2 = 3
- Add the numerators of the fractions: 8 + 5 = 13
Video – Dividing by fractions
Watch this video to learn what reciprocals are and how this helps to divide by fractions.
Dividing by fractions.
Dividing by a number is equivalent to multiplying by the reciprocal of that number.
But what's a reciprocal?
The reciprocal of any fraction is that same fraction, with the numerator and denominator flipped.
For example, the reciprocal of 5 over 8 is 8 over 5, and vice versa.
You can write any integer, or whole number, as a fraction by placing it over a denominator of 1.
So, 3 is equivalent to 3 over 1. The reciprocal of 3 is, therefore, 1 over 3, and the reciprocal of 1 over 3 is 3 over 1, or just 3.
So, dividing by a number is equivalent to multiplying by the reciprocal of that number, means that, for example, 4 divided by 1 over 2 is equivalent to 4 multiplied by 2 over 1, or just 2. Where 2 is the reciprocal of 1 over 2.
Let's look at some example questions:
First, calculate 15 divided by 3 over 8.
This calculation is equivalent to 15 multiplied by the reciprocal of 3 over 8, which is found by flipping the numerator and the denominator to get 8 over 3.
It can be helpful to rewrite 15 as the fraction 15 over 1, before doing the multiplication.
This can then be rewritten as 15 multiplied by 8, all over 1, multiplied by 3.
15 multiplied by 8 equals 120, and 1 multiplied by 3 equals 3. Then, 120 divided by 3 equals 40.
The next question is: 5 over 3 divided by 5 over 6.
Pause the video here and have a go.
This can be rewritten as 5 over 3, multiplied by 6 over 5. Which equals 30 over 15, which equals 2.
How to multiply and divide fractions and mixed numbers
Look at the examples below on how to multiply and divide fractions and mixed numbers.
Mixed numbers are written as A fraction where the numerator is greater than the denominator, eg ⁹⁄₄. before any multiplication or division.
How to multiply fractions:
- Multiply the Number written at the top of a fraction. The numerator is the number of parts used, eg for ⅓, the numerator is 1..
- Multiply the Number written on the bottom of a fraction. The denominator is the number of equal parts, eg for ⅓, the denominator is 3..
How to divide fractions:
- Multiply by the Written as 1 divided by the number, eg the reciprocal of 2 is ½ and the reciprocal of ½ is 2. The reciprocal is also called the multiplicative inverse. Any non-zero number multiplied by its reciprocal is equal to one. of the second fraction.
If possible, simplify the fractions before carrying out further working.
Finally, To reduce a fraction to its simplest form, also known as its lowest terms. your answer.
GCSE exam-style questions
- Work out this division:
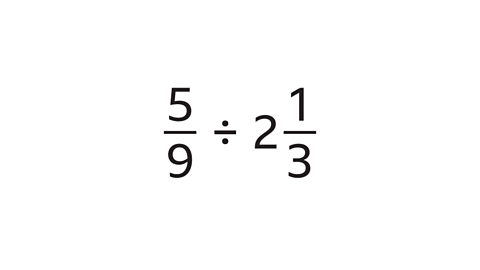
\(\frac{15}{63}\) (\(\frac{5}{21}\) when simplified).
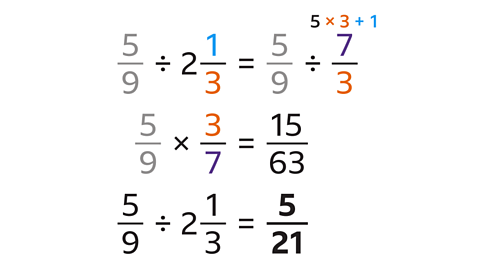
- Convert the mixed number into an improper fraction:
- The numerator of the improper fraction is
2 × 3 + 1 = 7 - The denominator is 3.
- The numerator of the improper fraction is
- Invert the second fraction.
- \(\frac{7}{3}\) becomes its reciprocal \(\frac{3}{7}\)
- Multiply the numerators: 5 × 3 = 15
- Multiply the denominators: 9 × 7 = 63
- Simplify by dividing the numerator (15) and denominator (63) by their HCF (3):
\(\frac{5}{9}\) ÷ \(2\frac{1}{3}\) = \(\frac{5}{21}\)
- Find the product of these fractions:
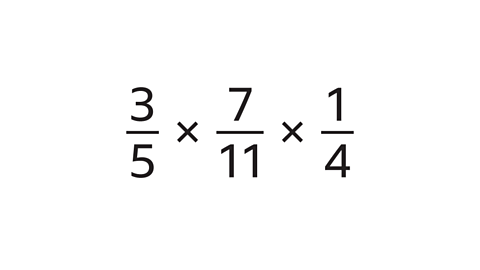
\(\frac{21}{220}\)
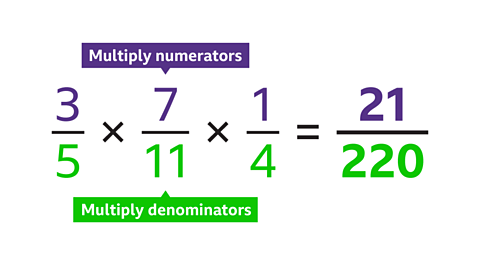
- Multiply the numerators: 3 × 7 × 1 = 21
- Multiply the denominators: 5 × 11 × 4 = 220
\(\frac{3}{5}\) × \(\frac{7}{11}\) × \(\frac{1}{4}\) = \(\frac{21}{220}\)
How to use a calculator for fractions
To enter a fraction using the fraction button:
- Enter the Number written at the top of a fraction. The numerator is the number of parts used, eg for ⅓, the numerator is 1..
- Press the fraction function button (see image).
- Enter the Number written on the bottom of a fraction. The denominator is the number of equal parts, eg for ⅓, the denominator is 3..
or - Press the fraction function button.
- Enter the numerator.
- Navigate down (▼).
- Enter the denominator.
To enter more of a calculation, move right using the navigation button (►).
To enter a mixed number using the mixed number button:
- Enter the integer.
- Press the mixed number function button (see image).
- Enter the numerator.
- Navigate down (▼).
- Enter the denominator.
or - Press the mixed number function button.
- Enter the integer.
- Navigate right (►).
- Enter the numerator.
- Navigate down (▼).
- Enter the denominator.
To enter more of a calculation, move right using the navigation button (►).
Follow the working out below
GCSE exam-style questions
- The addition \(\frac{1}{2} + \frac{1}{4}\) is entered into a calculator.
The answer should be \(\frac{3}{4}\) but the fraction on the calculator is different.
How should the calculation be entered to get the correct answer?
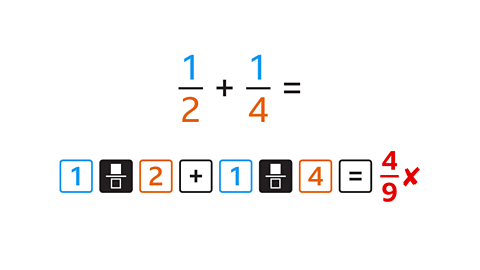
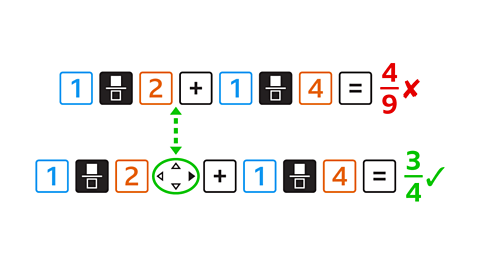
After the first fraction has been entered, the navigation key should be pressed so that the addition is separate from the fraction.
This will give the correct answer.
2. Use a calculator to find the answer to this multiplication:
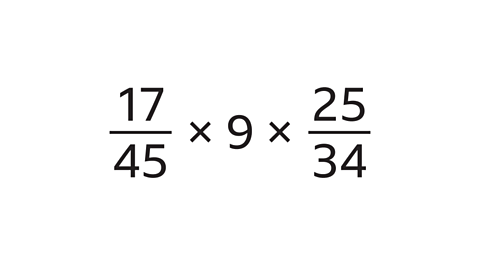
2·5 (or 2½)
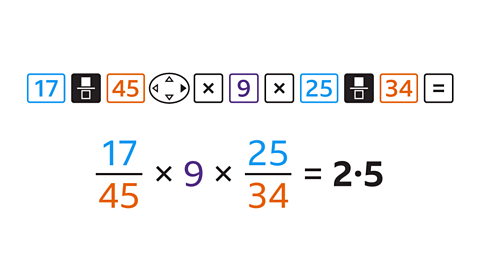
Press the buttons:
→ 17→ fraction button → 45
→ navigate right (►)
→ multiply (×)
→ 9
→ multiply (×)
→ 25 → fraction button → 34
→ equals (=)
The answer is 2·5 (2½).
This may be displayed on the calculator as \(\frac{5}{2}\).
How to find the fraction of an amount
To find a fraction of an amount:
- Divide the amount by the Number written on the bottom of a fraction. The denominator is the number of equal parts, eg for ⅓, the denominator is 3..
- Multiply the answer by the Number written at the top of a fraction. The numerator is the number of parts used, eg for ⅓, the numerator is 1..
If the denominator does not divide exactly into the amount, use a calculator or multiply by the numerator and then divide by the denominator using division skills.
Follow the working out below
GCSE exam-style questions
- Find \(\frac{3}{5}\) of 90.
\(\frac{3}{5}\) of 90 is 54.
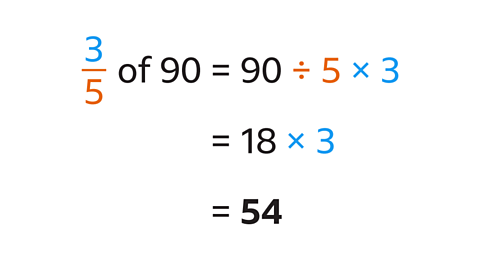
- Divide the amount (90) by the denominator (5):
- 90 ÷ 5 = 18
- Multiply 18 by the numerator (3):
- 18 × 3 = 54
- Find \(\frac{3}{7}\) of 20.
Give the answer as a mixed number.
\(\frac{3}{7}\) of 20 is \(8\frac{4}{7}\).
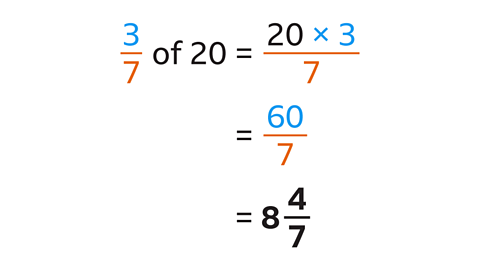
The denominator (7) does not divide exactly into the amount (20).
Multiply the amount (20) by the numerator (3).
Then divide by the denominator (7) using division skills.
- 20 multiplied by 3 is 60.
- 60 divided by 7 is 8 remainder 4, this gives \(8\frac{4}{7}\).
Quiz - Fractions
Practise what you've learned about fractions with this quiz.
Now you've revised how to add, subtract, multiply and divide fractions, why not try learning about fractions, decimals and percentages?
More on Number
Find out more by working through a topic
- count10 of 15
- count12 of 15
- count13 of 15
