Decimal place values
We use a decimal point to separate units from parts of a whole, such as tenths, hundredths, thousandths, etc.
- \({0.1}\) is a tenth, \(\frac{1}{10}\), of a unit
- \({0.01}\) is a hundredth, \(\frac{1}{100}\), of a unit
- \({0.001}\) is a thousandth, \(\frac{1}{1,000}\), of a unit
In \({52.13}\), the value of the \({1}\) is one tenth or \(\frac{1}{10}\), and the value of the digit \(3\) is three hundredths or \(\frac{3}{100}\).
Ordering decimals
When ordering numbers, always compare the left digits first.
For example, which is greater \({2.301}\) or \({2.32}\)?
Both numbers have two units and three tenths, but \({2.301}\) has no hundredths, whereas \({2.32}\) has two hundredths.
Therefore, \({2.32}\) is greater than \({2.301}\).
Adding a zero
Another way to look at it is to add a zero to the end of \({2.32}\).
This doesn't change the value as it is after the decimal point.
This means that both numbers will have the same number of digits after the decimal point.
The two numbers are now \({2.320}\) and \({2.301}\).
It is easier to see that \({2.320}\) is bigger - just as \({2,320}\) is bigger than \({2,301}\).
Questions
Q1. In the number \(3.546\), what is the value of the digit \(4\)?
Q2. Place the following numbers in order, smallest first: \(3.2\), \(3.197\), \(3.02\), \(3.19\)
Answers
A1. The value of the digit \(4\) is four hundredths, or \(\frac{4}{100}\).
A2. Did you get \(3.02\), \(3.19\), \(3.197\), \(3.2\)?
All the numbers have three units, so start by comparing the tenths. \(3.02\) has no tenths, \(3.197\) and \(3.19\) have one tenth, and \(3.2\) has two tenths. Therefore, \(3.02\) is the smallest and \(3.2\) is the largest.
When comparing \(3.197\) and \(3.19\), both have \({9}\) hundredths. \(3.19\) has no further digits, but \(3.197\) also has \({7}\) thousandths, meaning that \(3.19\) is smaller than \(3.197\).
You can add zeros to the ends of the numbers and so write the numbers as \(3.020\), \(3.190\), \(3.197\) and \(3.200\) and compare them.
Adding and subtracting decimals
When adding and subtracting decimals, remember to keep the decimal points in line in the question and the answer.
Question
David is doing some DIY.
He buys a \({2}~m\) length of wood.
He needs to cut two pieces of wood - one of length \({0.6}~m\) and one of length \({1.02}~m\).
What is the total length of wood that David needs to cut?
Answer
Add \(0.6\) and \(1.02\)
So the total length of wood that David needs to cut is \({1.62}~m\).
Key point
You can add zeros to the end of a decimal without affecting its value, so 0.6 is the same as 0.60.
Subtracting decimals
Question
David originally had \({2}~m\) of wood.
What is the length of the piece of wood that is left over?
Answer
You can add zeros after a decimal point without affecting its value, so \({2}\) is the same as \({2.00}\).
David cut off \({1.62}~m\), so we need to calculate \(2 - 1.62\)
This means that there is \({0.38}~m\) of wood left over.
Multiplying decimals by 10, 100 and 1,000
Multiplying a decimal by 10
When a decimal is multiplied by \({10}\), each digit moves one place to the left.
Multiplying a decimal by 10

Image caption, What is 4.25 × 10?
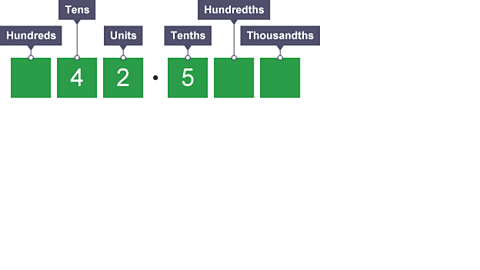
Image caption, Each digit moves 1 place to the left, so 4.25 × 10 = 42.5
1 of 2
Multiplying a decimal by 100
When multiplying by \({100}\), each digit moves two places to the left.
Multiplying a decimal by 100
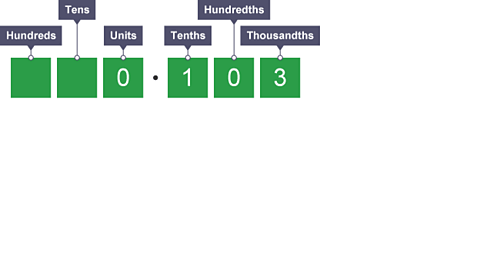
Image caption, What is 0.103 × 100?

Image caption, Each digit moves 2 places to the left. The zero at the front is no longer needed so we ignore it. Therefore 0.103 × 100 = 10.3
1 of 2
Multiplying a decimal by 1,000
When multiplying by \({1,000}\), each digit moves three places to the left.
Multiplying a decimal by 1000
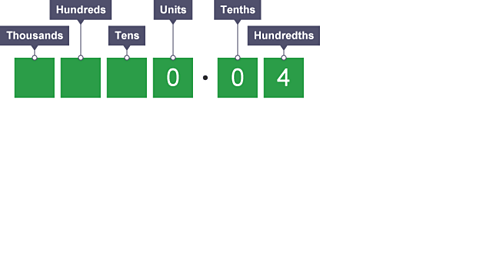
Image caption, What is 0.04 × 1,000?
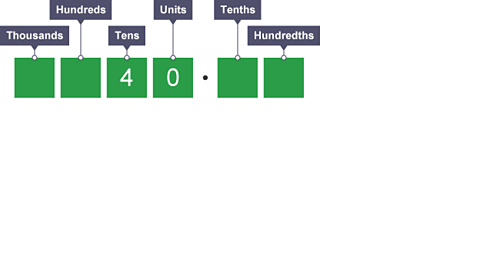
Image caption, Each digit moves 3 places to the left. The two zeros in the thousands and hundreds columns are no longer needed so we ignore them. We don't have any units, so we place a '0' in the units column. Therefore we get 0.04 × 1,000 = 40.
1 of 2
Question
Which is bigger: \(0.005 \times 10\) or \({0.0004}\times{1,000}\)?
Answer
The answer is \({0.0004}\times{1,000}\)
If your answer is incorrect, remember that multiplying by \({10}\) moves each digit one place to the left.
Therefore, \(0.005 \times 10 = 0.05\).
Multiplying by \(1,000\) moves each digit three places to the left.
Therefore, \({0.0004}\times{1,000} = {0.4}\).
\(0.4\) is bigger than \(0.05\).
Dividing decimals by 10, 100, 1,000
Dividing a decimal by 10
When you divide by \(10\), each digit moves one place to the right.
Hundreds become tens, tens become units, units become tenths and tenths become hundredths.
Dividing by 10
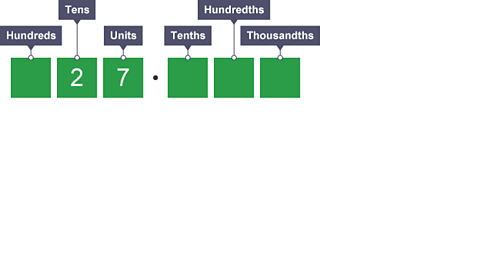
Image caption, What is 27 divided by 10?

Image caption, Each digit moves 1 place to the right. Therefore 27 ÷ 10 = 2.7
1 of 2
Dividing a decimal by 100
When you divide by \({100}\), each digit moves two places to the right.
Dividing by 100
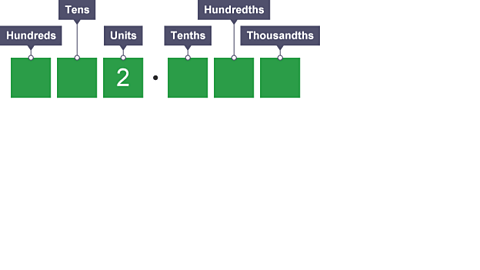
Image caption, What is 2 divided by 100?
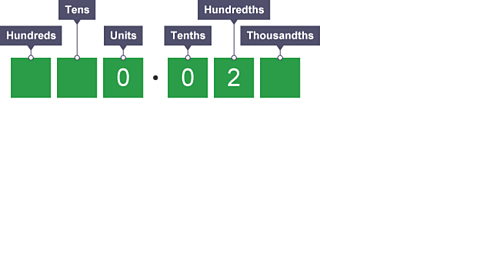
Image caption, Each digit moves 2 places to the right. We don't have any units and tenths, so we place a '0' in the columns. Therefore 2 ÷ 100 = 0.02.
1 of 2
Dividing a decimal by 1000
When you divide by \({1,000}\), each digit moves three places to the right.
Dividing by 1000
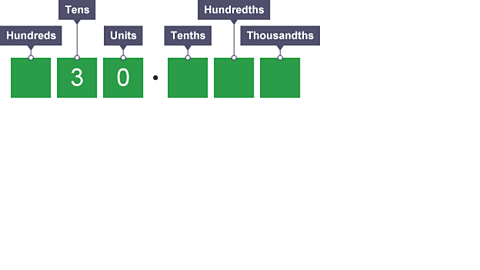
Image caption, What is 30 divided by 1,000?
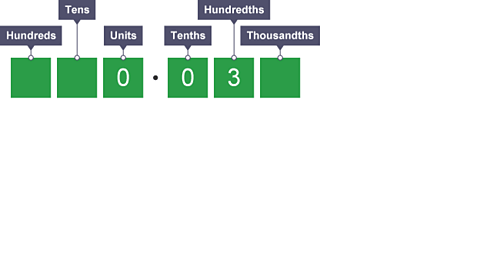
Image caption, Each digit moves 3 places to the right. We don't have any units and tenths, so we use '0' in each column. A zero in the thousandths column is not needed so we ignore it. Therefore 30 ÷ 1,000 = 0.03.
1 of 2
Multiplying a decimal by a whole number
Multiplying a decimal by a whole number uses the same method as multiplying two whole numbers.
Question
Calculate:
a) \(2.43 \times 7\)b) \(2.4 \times 5\)
Answer
a) There were two digits after the decimal point in the question \((4\) and \(3)\), so you must have two digits after the decimal point in the answer.
b) There was one digit after the decimal point in the question \((4)\), so you must have one digit after the decimal point in the answer.
The answer is therefore \(12.0\), but this can then be given as \(12\)
Remember:
- If there is one digit after the decimal point in the question, there will be one digit after the decimal point in the answer.
- If there are two digits after the decimal point in the question, there will be two digits after the decimal point in the answer.
Check that you have the correct answer by finding an approximate solution.
In the above example you were asked to calculate \(2.4 \times 5\).
\({2}\times{5}={10}\) and \({3}\times{5}={15}\), so you are looking for an answer which is slightly higher than \({10}\).
So an answer of \({12}\) seems correct.
Dividing a decimal by a whole number
Remember to keep the decimal points aligned in the question and the answer.
Example
Work out \(4.05\) divided by \({9}\)
Solution
Example
Work out \(2.4\) divided by \(5\)
Solution
Key point
It is sometimes necessary to add a zero to the end of a decimal, as in this example (2.4 is the same as 2.40 but the question stays the same).
Learn about the 'point' of decimals when weighing your holiday luggage
How important are units, tenths and hundredths?
Antoine Bonjour and welcome to Squeezey Jet. Passports please. Hmmm… Ok. Pop your suitcase on here please Madame.
Mattsmutt Uh-oh.
Sophie But I weighed my case at home. My clothes were 9kg. My gadgets and books were 2kg. And my case was 4kg. That’s 15kg!
Mattsmutt Let’s break it down.
Sophie See? My suitcase weighs 4kg!
Mattsmutt Wrong Sophie. Look closer. The needle is between 4 and 5, so it’s more than 4kg.
We can split each unit into 10 more units, or ‘tenths’, because there’s 10 of them between the 4 and the 5.
We write that as “1/10”
Sophie A-ha! So it’s 4 and 2 tenths.
Mattsmutt Yep. And we can call that 4.2kg. Now, let’s try your clothes.
Sophie Hey, it’s not 9kg at all. My clothes weigh 9.3kg!
Mattsmutt Hmmm. I think we’d better investigate.
We can even split the tenths into 10.
And we call those hundredths because there’s 100 of them between the 9 and the 10.
So your clothes actually weigh 9kg, 3 tenths and 4/100ths. Or, 9.34kg.
Sophie Ok. Let’s try my gadgets and books.
Mattsmutt Wowzers. It’s 2kg plus 4/10ths and 8/100ths.
That’s 2.48kg!
Sophie No wonder my suitcase is too heavy.
Mattsmutt Let’s work out how we add them all together. It’s important to keep the decimal points in a vertical line, and don’t worry about some having more numbers than others.
Sophie Ok. So my suitcase was 4.2kg. My clothes were 9.34kg. And my gadgets and books were 2.48kg.That makes 16.02kg!
Mattsmutt Correctamundo! Elementary my dear Sophie!
But you’ll have to take something out. What about that copy of the Gone Direction boy-band annual?
Sophie Errr. What copy of the Gone Direction boy-band annual?
Antoine C’est magnifique! Your tickets Madame. Bon voyage!
Sophie Thanks for your help Mattsmutt… Mattsmutt?
Mattsmutt So, did our investigation help you see the ‘point’ of decimals?
Sophie Yes Mattsmutt. It was an open and shut case. Haha
Antoine Ooh la la. J’adore Gone Direction.
Test section
Question 1
Which of the following is the biggest number: \({2.107}\), \({2.7}\) or \({2.21}\)?
Answer
Look at the value of the digits starting from the left. \({7~tenths}\) is bigger than \({1~tenth}\) and \(<{2~tenths}\), no matter how many digits follow.
So \({2.7}\) is the biggest number.
Question 2
What's the value of the figure \({4}\) in the number \({2.45}\)?
Answer
The value of the first digit after the decimal point is a tenth (\(\frac{1}{10}\)).
So the correct answer is \({4~tenths}\).
Question 3
Calculate \({4.15}+{6.2}\)
Answer
Add a \({0}\) at the end of \({6.2}\) to help add up the numbers.
The answer is \({10.35}\).
Question 4
Calculate \({6.7}-{3.27}\)
Answer
Add \({0}\) at the end of \({6.7}\) in order to subtract in a column and get the answer \({3.43}\).
Question 5
An exercise book costs \({89}{p}\).
What is the price of \({10}\) exercise books?
Answer
When multiplying by \({10}\) each digit moves one place to the left.
Here, \({89}{p}=\pounds{0.89}\) multiplied by \({10}\) is \(\pounds{8.90}\).
Question 6
Calculate \({8.13}\times{1,000}\)
Answer
Each digit moves three places to the left when multiplying by \({1,000}\).
Here, \({8.13}\times{1,000}={8,130}\).
Question 7
Calculate \({6.1}\div{100}\)
Answer
Each digit moves two places to the right when dividing by \({100}\).
Here, \({6.1}\div{100}={0.061}\).
Question 8
The thickness of \({1,000}\) sheets of paper is \({25}~{cm}\).
What is the individual thickness of each sheet?
Answer
Each figure moves three places to the right when you divide by \({1,000}\).
Here, \({25}~{cm}\div{1,000}={0.025}~{cm}\).
Question 9
Calculate \({4.56}\times{3}\)
Answer
There are two digits after the decimal point in the question, so there should be two digits after the decimal point in the answer too.\({456}\times{3}={1,368}\), so \({4.56}\times{3}={13.68}\).
Question 10
The bill in a cafe comes to \(\pounds{5.55}\).
Three friends want to share the cost equally.
How much should each one pay?
Answer
Divide \(\pounds{5.55}\) by \({3}\) to get how much each friend has to pay:
\(\pounds{5.55}\div{3}=\pounds{1.85}\).