Key points about calculations using standard form

- Add or subtract numbers in standard formA number between 1 and 10 multiplied by a power of ten, eg 193 in standard form is written as 1·93 × 10², 0·193 in standard form is written as 1·93 ×10⁻¹. It is used as notation for very large and very small numbers. It is also called standard index form or scientific notation. using decimal number format or by matching the power of tenThe power of ten tells us how many times to use the number in a multiplication. For example 10² means 10 × 10 = 100. Powers of ten are 10, 100, 1000 and so on. .
- Multiply or divide numbers in standard form by processing them within standard form format.
Support your knowledge of this topic with these guides on standard form and the laws of indices.
Video – Calculating in standard form
Watch this video to see how to work out calculations using standard form by following worked practice questions.
Calculating in standard form.
Let's look at some calculations using standard form.
This question asks you to work out 3 times 10 to the power of 2 multiplied by 4 times 10 to the power of 5.
Give your answer in standard form.
In multiplication, you can rearrange the calculation in any order and still get the same answer. So, rearrange the calculation to give 3 times 4, times 10 to the 2, times 10 to the 5.
Firstly, 3 times 4 is 12. Then, to work out the second product, 10 to the 2 times 10 to the 5 you need to use the laws of indices.
When multiplying indices with the same base you add the powers together. So, 10 to the 2 times 10 to the 5 equals 10 to the power of 2 add 5, which is 10 to the power of 7.
You now have 12 times 10 to the power of 7. But notice 12 isn't between 1 and 10, so this isn't in standard form yet. The first number in standard form must be between 1 and 10. So this has to be 1.2. Moving the digits one place left is equivalent to multiplying by 10 to the 1. So, 12 written in standard form is 1.2 times 10 to the 1.
Putting this into the answer gives 1.2 times 10 to the 1 times 10 to the 7. Then, using the multiplication index law again, this simplifies to 1.2 times 10 to the power of 1 add 7, which equals 1.2 times 10 to the power of 8.
Let's look at another question.
This one asks you to work out 3 times 10 to the power of 2 divided by 4 times 10 to the power of 5.
Give your answer in standard form.
Rewriting this as a fraction shows that you can rearrange the calculation to give 3 divided by 4, multiplied by 10 to the 2, divided by 10 to the 5.
3 divided by 4 equals 0.75. Then, to calculate 10 to the 2 divided by 10 to the 5, use the index law for division which says you subtract the powers. So, this equals 10 to the power of –3.
0.75 times 10 to the power of –3 is not in standard form, as 0.75 is not between 1 and 10. The first number must be 7.5.
Moving in digits one place right is equivalent to multiplying by 10 to the –1. So 0.75, written in standard form, is 7.5 times 10 to the –1.
Putting this into the answer, and using the multiplication index law, this gives a final answer of 7.5 times 10 to the power of – 4.
Check your understanding
How to add and subtract in standard form without a calculator
To add or subtract in standard form using ordinary numbers:
- Convert each number from standard form to an ordinary number.
- Perform the addition or subtraction.
- Convert the answer back into standard form.
To add or subtract in standard form by working in standard form:
- Rewrite the values so that the numbers use the lower power of tenThe power of ten tells us how many times to use the number in a multiplication. For example 10² means 10 × 10 = 100. Powers of ten are 10, 100, 1000 and so on. .
For example, for a problem involving 10² and 10⁷, 10² is a lower power of ten than 10⁷. - Rewrite the calculation as an addition or subtraction multiplied by the power of ten.
- Write the answer to the calculation multiplied by the power of ten.
- Make sure the final answer is written correctly in standard form.
To correct numbers written improperly in standard form:
- Write the number in standard form multiplied by the power of ten.
- Simplify the powers of ten by adding the index (plural indices)Positioned above and to the right of a number. It is an abbreviation of repeated multiplication, eg 7³ means 7 × 7 × 7. An index may be positive, negative, zero or fractional. Indices are also referred to as powers or exponents..
GCSE exam-style questions
- Find the difference between (8 × 10⁻² and (8 × 10⁻³).
Give the answer as a decimal.
0·072
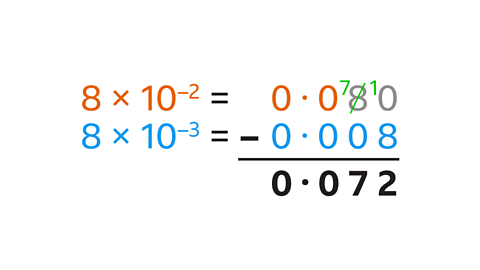
- Convert each number from a standard form number to an ordinary number:
- 8 × 10⁻² = 0·08
- 8 × 10⁻³ = 0·008
- The two decimal numbers are subtracted:
- 0·08 – 0·008 = 0·072
(8 × 10⁻²) – (8 × 10⁻³) = 0·072
- Work out (9·2 × 10¹⁵) + (1·54 × 10¹⁵).
Give the answer in standard form.
1·074 × 10¹⁶
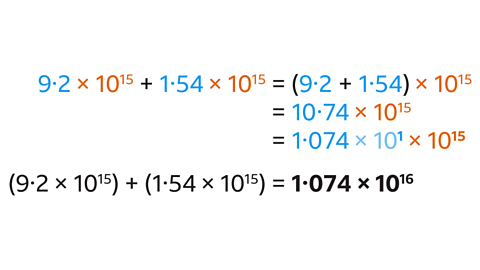
- The powers of ten are the same, so add the decimals:
- (9·2 + 1·54) ×10¹⁵ = 10·74 ×10¹⁵
This number is not in standard form.
- Write 10·74 in standard form:
- 1·074 × 10¹
- Multiply by 10¹⁵
- Use the laws of indices (add the indices).
(9·2 × 10¹⁵) + (1·54 × 10¹⁵) = 1·074 × 10¹⁶
How to multiply and divide in standard form without a calculator
To multiply numbers in standard formA number between 1 and 10 multiplied by a power of ten, eg 193 in standard form is written as 1·93 × 10², 0·193 in standard form is written as 1·93 ×10⁻¹. It is used as notation for very large and very small numbers. It is also called standard index form or scientific notation.:
- Multiply the values of 𝐴.
- Multiply the power of tenThe power of ten tells us how many times to use the number in a multiplication. For example 10² means 10 × 10 = 100. Powers of ten are 10, 100, 1000 and so on. by adding the index (plural indices)Positioned above and to the right of a number. It is an abbreviation of repeated multiplication, eg 7³ means 7 × 7 × 7. An index may be positive, negative, zero or fractional. Indices are also referred to as powers or exponents..
- Write the answer in standard form.
To divide numbers in standard form:
- Write the calculation as a fraction.
- Divide the values of 𝐴.
- Divide the powers of ten by subtracting the indices.
- Write the answer in standard form.
GCSE exam-style questions
- Work out (5 ×10⁸) by (6 ×10⁸).
Give your answer in standard form.
3 × 10¹⁷
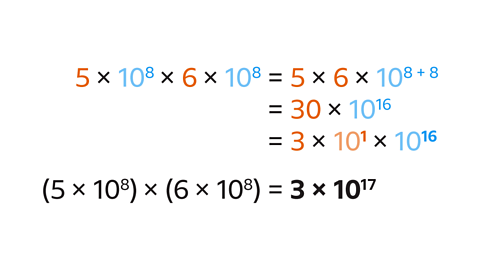
- Multiply the values of 𝐴: 5 × 6 = 30
- Multiply the powers of ten (add the indices):
- 10⁸ × 10⁸ = 10¹⁶
The answer 30 × 10¹⁶ is not in standard form.
- Write 30 in standard form:
- 30 is 3 × 10¹
- Multiply 10¹ and 10¹⁶ together (add the indices):
- 10¹ × 10¹⁶ = 10¹⁷
(5 × 10⁸) × (6 × 10⁸) = 3 × 10¹⁷
- Complete the calculation (3∙6 × 10⁻⁶) ÷ (2 × 10⁻⁴).
Give the answer as an ordinary number.
0·018
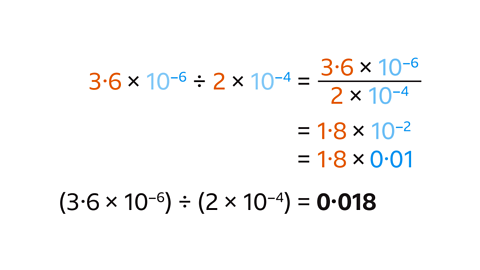
- Write the calculation as a fraction:
- 3·6 × 10⁻⁶ is the numerator.
- 2 × 10⁻⁴ is the denominator.
- Divide the values of 𝐴:
- 3·6 ÷ 2 = 1·8
- Divide the powers of ten (subtract the indices):
- 10⁻⁶ ÷ 10⁻⁴ = 10⁻²
The answer 1·8 × 10⁻² is in standard form.
- Convert to an ordinary number: 1·8 × 10⁻²
- This is the same as 1·8 × 0·01 or dividing 1·8 by ten twice.
1·8 × 10⁻² = 0·018
How to calculate standard form with a calculator
On a scientific calculator there is a specific button used for standard formA number between 1 and 10 multiplied by a power of ten, eg 193 in standard form is written as 1·93 × 10², 0·193 in standard form is written as 1·93 ×10⁻¹. It is used as notation for very large and very small numbers. It is also called standard index form or scientific notation.. The button may look different on different makes of calculator.

To enter 𝐴 × 10\(^n\):
- Enter the value of 𝐴.
- Press the standard form button.
- Enter the value of 𝑛.
Using the ×10\(^x\), EXP or EE button will keep the whole number together, including the ‘times-ten-to-the-power’ part, so no brackets are needed when using that number in a calculation.
Revise how to use a calculator for further support.

GCSE exam-style questions
- Use a calculator to work out this calculation.
Give the answer in standard form.
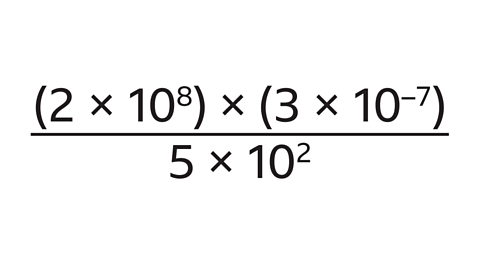
1·2 ×10⁻¹
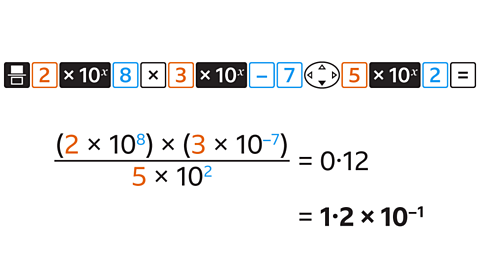
On a scientific calculator, the calculation can be entered using the fraction button and the standard form button:
→ Fraction button
Enter the numerator:
→ 2 → standard form button → 8
→ multiply (×)
→ 3 → standard form button → –7
→ Navigate down (▼)
Enter the denominator:
→ 5 → standard form button → 2
→ equals (=)
If your answer is shown as a fraction, change the format to decimal.
The answer is 0·12, which is 1·2 ×10⁻¹ in standard form.
- Use a calculator to work out:
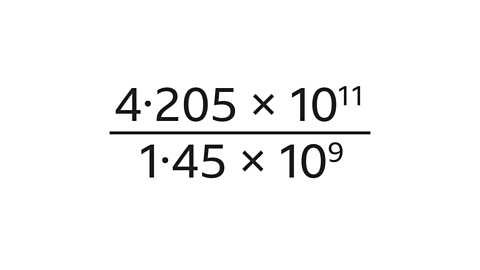
290
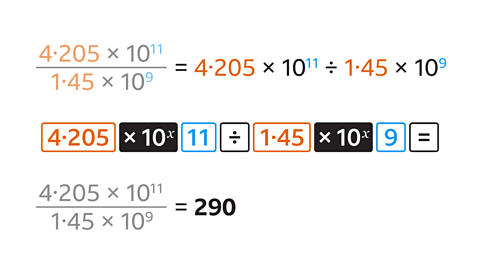
The calculation is a division:
→ 4·205 → standard form button → 11
→ divide (÷)
→ 1·45 → standard form button → 9
→ equals (=)
The question does not state what form the answer should be in, so an ordinary number is an appropriate answer.
Quiz – Calculations using standard form
Practise what you've learned about calculations using standard form with this quiz. The questions change each time you try, so keep testing your knowledge.
Now you've revised calculations using standard form, why not try looking at how to round numbers?
More on Number
Find out more by working through a topic
- count1 of 15

- count2 of 15

- count3 of 15
