What is translation?
In geometry, the word translation means moving.
It can help to think of translating a shape as sliding the shape.
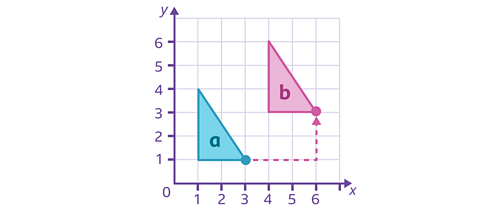
When you translate a shape:
- every point on the shape moves the same distance and in the same direction.
- the size of the shape stays the same.
- the shape is not rotated - its orientation stays the same.
The original shape and the resulting images are congruent, which means they have the same shape and size.
Activity: Translating in four quadrants
Discover how to translate a shape in this interactive activity and then put your knowledge to the test with a quiz.
How to translate shapes in four quadrants
In geometry, translating a shape means moving it without changing its size, shape or orientation.
You can translate a shape on a grid by sliding it to a new position.
You can move the shape left or right on the x-axis and up and down on the y-axis.
If the shape is in a four quadrant grid like this one, there might be negative coordinates as well.
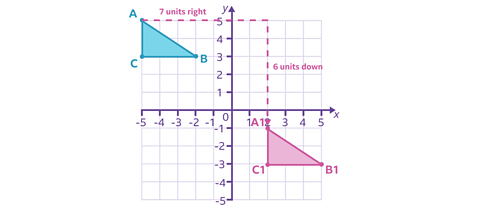
On this grid, the position of the blue triangle has been translated to a new position to make the pink triangle.
The blue triangle's top corner marked point A starts at (-5, 5). It moves 7 units right and then 6 units down, it ends up at (2, -1) as point A1 on the pink triangle.
You do not need to count on the grid to work out new coordinates. You can use your understanding of the x- and y-axis to find out the new coordinates.
Moving a shape left or right changes the x-coordinates, while moving it up or down changes the y-coordinates.
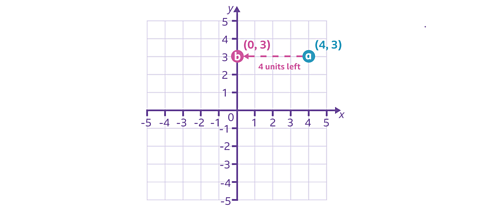
For example, if a point at (4, 3) is moved 4 units left, you subtract 4 from the x-coordinate, making it 0.
If it moved 4 units right, you add 4 to the x-coordinate, make it 8.
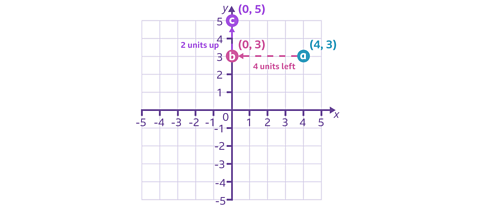
If the same point is then moved 2 units up, you add 2 to the y-coordinate, making it 5.
Or if you moved it 2 units down, you subtract 2 from the y-co-ordinate, making it 1.
Example 1
Take a look at the two triangles on this grid.
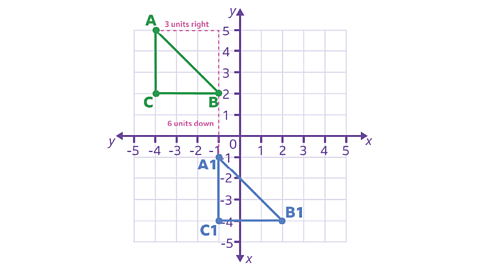
The right-angled triangle ABC is positioned in the second quadrant.
The coordinates of the triangle are:
| Point | Coordinates |
|---|---|
| A | -4, 5) |
| B | (-1, 2) |
| C | -4, 2) |
The triangle ABC is translated 3 units to the right (parallel to the x-axis) and 6 units down (parallel to the y-axis)
What are the coordinates of the new triangle A¹B¹C¹?
✓ The resulting image of this translation has been labeled A¹B¹C¹.
This means the new coordinates are:
| Point | Coordinate |
|---|---|
| A¹ | (-1, -1) |
| B¹ | (2, -4) |
| C¹ | (-1, -4) |
The triangle ABC and the triangle A¹B¹C¹ are congruent.
Congruent means that the two shapes have the same size and the same shape.
Example 2
Now, here are the points of a parallelogram plotted on a grid.
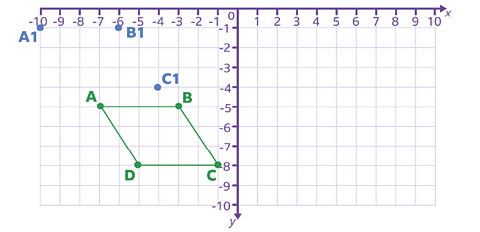
The coordinates of the parallelogram are:
| Point | Coordinates |
|---|---|
| A | (-7, -5) |
| B | (-3, -5) |
| C | (-1, -8) |
| D | -5, -8) |
The parallelogram is translated 3 units to the left (parallel to the x-axis) and 4 units up (parallel to the y-axis).
Here are the new coordinates for three of the points:
| Point | Coordinates |
|---|---|
| A¹ | (-10, -1) |
| B¹ | (-6, -1)) |
| C¹ | (-4, -4) |
| D¹ | ? |
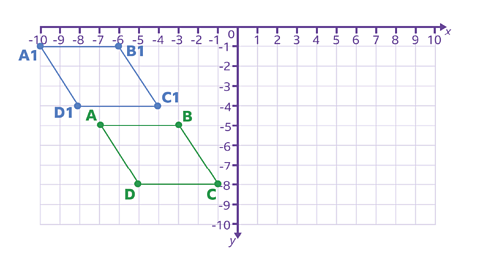
What will be the new coordinate for point D?
✓ Let's work it out step by step.
The starting coordinates for D are (-5, -8).
First let's translate 3 units to the left.
Move the coordinate 3 units to the left on the grid or subtract 3 from the x-coordinate.
-5 - 3 = -8
Now let's translate 4 units up.
Move the coordinate 4 units up on the grid or add 4 to the y-coordinate.
-8 + 4 = -4
So, the new coordinates for point D are D¹ (-8, -4).
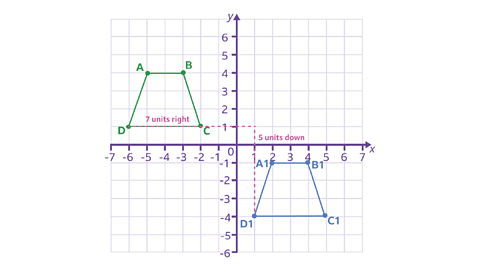
Example 3
Here are two trapeziums plotted on a grid.
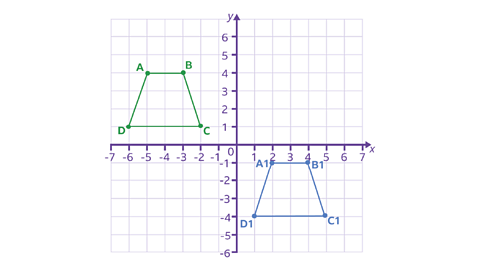
The trapezium ABCD is positioned in the second quadrant.
The coordinates of the trapezium are:
| Point | Coordinates |
|---|---|
| A | (-5, 4) |
| B | (-3, 4) |
| C | (-2, 1) |
| D | (-6, 1) |
After a translation, the new coordinates are:
| Point | Coordinates |
|---|---|
| A¹ | (2, -1) |
| B¹ | (4, -1) |
| C¹ | (5, -4) |
| D¹ | (1, -4) |
But, how has it been translated?
✓ The new coordinates of D¹ are (1, -4).
Let's look at the x coordinate first.
It went from -6 to 1. Look on the grid, which direction has it moved in?
It's moved 7 units to the right.
Now let's look at the y coordinate.
It went from 1 to -4. Look on the grid, which direction is that?
It's moved down by 5 units.
You can check this with other points to make sure.
The trapezium ABCD was translated 7 units to the right and 5 units down.
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Coordinates
Find out more by working through a topic
- count1 of 3

- count2 of 3
