KS3

Equivalent ratios and simplifying ratios

Part of MathsRatio

Key points

A states the comparison between two or more parts within a whole. The parts may be different or equal in size.
The notation for a ratio uses a colon to separate the numeric parts, eg 5 : 2
Ratios are usually written using , but not always.
Ratios may be by dividing the parts by their . The ratio 10 : 4 simplifies to 5 : 2, for example. To simplify ratios, knowledge of how to find the highest common factor (HCF) is useful.

What is a ratio?

A :

is the number of one part compared to the number of one or more other parts
is defined by the order of the values. 2 : 3 is not the same as 3 : 2
can be represented in words, numbers, or diagrams

A ratio can be related to fractions. Eg, in the ratio 2 : 3

the total number of ratio parts is 2 + 3 which is 5. This is the of the related fractions, \( \frac{2}{5} \) and \( \frac{3}{5} \)
the 2 parts are 2 out of a total of 5 parts (\( \frac{2}{5} \)). 2 is the
the 3 parts are 3 out of a total of 5 parts (\( \frac{3}{5} \)). 3 is the numerator

Examples

Skip image gallery

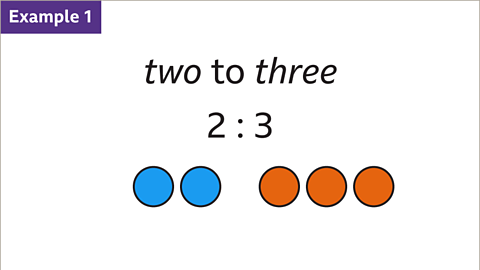
Image caption,
The ratio two to three (2 : 3) can be represented in words, numbers or diagrams.
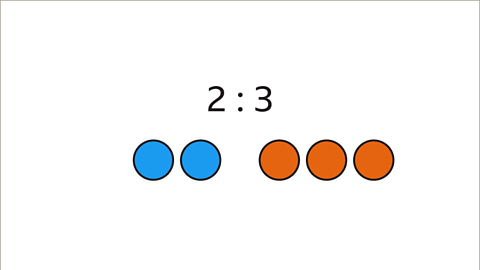
Image caption,
The ratio of the number of blue circles to the number of orange circles is 2 : 3. There are 2 blue circles for every 3 orange circles.
Image caption,
Now the ratio of the number of orange circles to the number of blue circles is 3 : 2. There are 3 orange circles for every 2 blue circles.
Image caption,
The ratio of the number of yellow circles to the number of white circles is 1 : 4. For each yellow circle there are 4 white circles. The ratio 3 : 12 is equivalent to 1 : 4 because for each yellow circle there are 4 white circles.
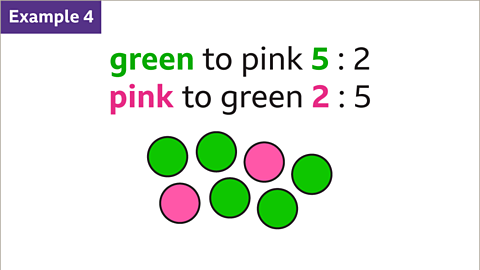
Image caption,
The order of the ratio is important. 5 : 2 is not the same as 2 : 5. For example, the ratio of green to pink circles is 5 : 2. The first colour (green) is represented by the first number (5). The ratio of pink to green is 2 : 5. The first colour (pink) is represented by the first number (2)
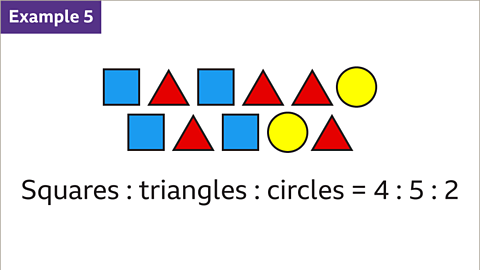
Image caption,
There are 4 squares, 5 triangles and 2 circles. The ratio of the number of squares to triangles to circles is 4 : 5 : 2
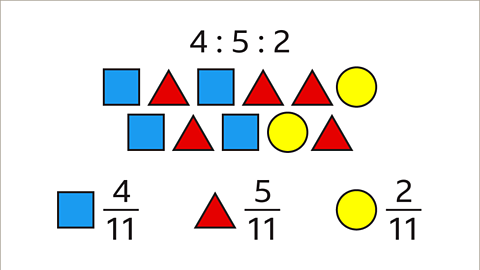
Image caption,
The ratio is linked to parts of a fraction – it states the parts of the whole (4 parts, 5 parts, 2 parts). The total number of parts in the ratio is 4 + 5 + 2 = 11. This gives the denominator of the fractions (11). The fraction of the shapes that are squares is 4⁄11. The fraction of shapes that are triangles is 5⁄11. The fraction of shapes that are circles is 2⁄11
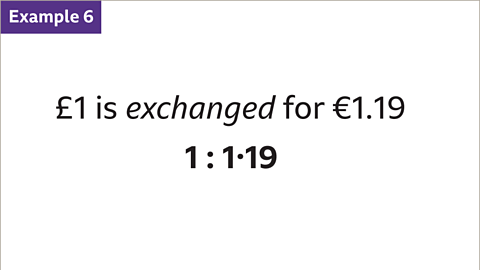
Image caption,
A ratio may sometimes be written using decimals, eg when exchanging currencies. This ratio shows that the exchange rate for Pounds sterling to Euros is £1 for €1.19

Question

A chef bakes some biscuits. They are shaped as stars, circles and squares in the ratio 2 : 7 : 4

What fraction of the biscuits are circles?

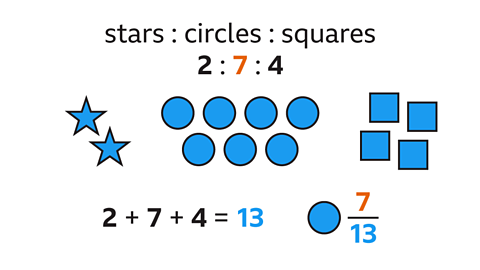
How to write equivalent ratios, including unitary ratios

have the same value as another. Each ratio represents the same part-to-part comparison.

To write an equivalent ratio, multiply or divide each part in the ratio by the same value.

are useful when solving proportion problems and finding the value of 1. Eg, £1 may be exchanged for a number of Euros - £1 : ? Euros. In this example, Euros is 𝒏

To write an equivalent unitary ratio in the form 1 : 𝒏, divide both parts in the ratio by the first part value.

To write an equivalent unitary ratio in the form 𝒏 : 1, divide both parts in the ratio by the second part value.

Example

Skip image gallery

Image caption,
Write equivalent ratios for 10 : 8
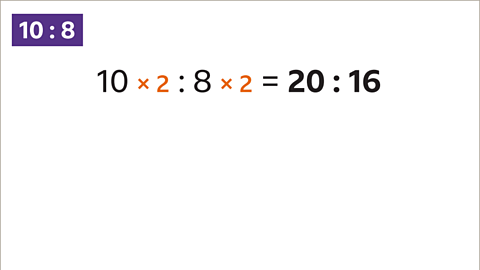
Image caption,
To write an equivalent ratio, multiply the parts by the same value. Here the 10 and the 8 are both multiplied by 2. 10 x 2 = 20. 8 x 2 = 16. 10 : 8 and 20 : 16 are equivalent ratios.
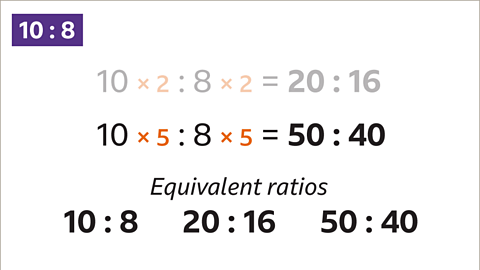
Image caption,
To write another equivalent ratio, multiply the parts by another value. Here the 10 and the 8 are both multiplied by 5. 10 x 5 = 50. 8 x 5 = 40. Another ratio that is equivalent to 10 : 8 is 50 : 40. 10 : 8 and 20 : 16 and 50 : 40 are equivalent ratios.
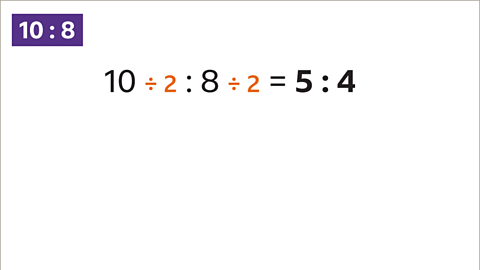
Image caption,
To write an equivalent ratio, you can also divide the parts by the same value. Here the 10 and the 8 are both divided by 2. 10 ÷ 2 = 5. 8 ÷ 2 = 4. 10 : 8 and 5 : 4 are equivalent ratios.
Image caption,
To write another equivalent ratio, divide the parts by another value. Here the 10 and the 8 are both divided by 5. 10 ÷ 5 = 2. 8 ÷ 5 = 1∙6. 10 : 8 and 5 : 4 and 2 ∶ 1∙6 are equivalent ratios.
Image caption,
Write 10 : 8 as a unitary ratio in the form 1 : 𝒏
Image caption,
To write an equivalent unitary ratio in the form 1 : 𝒏, both parts of the ratio (10 and 8) are divided by the first part value (10). 10 ÷ 10 is 1. 8 ÷ 10 is 0∙8. 10 : 8 is equivalent to the unitary ratio 1 : 0∙8
Image caption,
Write 10 : 8 as a unitary ratio in the form 𝒏 : 1
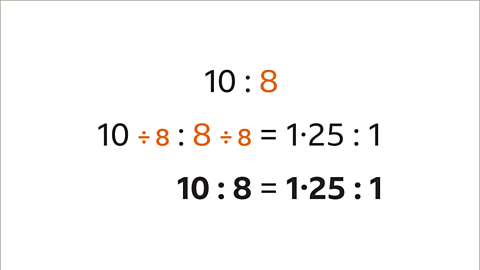
Image caption,
To write an equivalent unitary ratio in the form 𝒏 : 1, both parts of the ratio (10 and 8) are divided by the second part value (8). 10 ÷ 8 is 1∙25. 8 ÷ 8 is 1. 10 : 8 is equivalent to the unitary ratio 1∙25 : 1

Question

Complete the equivalent ratio for 6 : 18 : 20

Six to eighteen to twenty equals three to a blank box highlighted to a blank box highlighted.

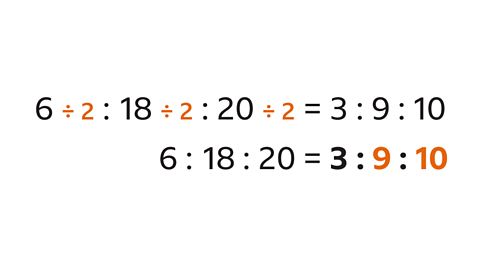
How to simplify ratios

The numbers in a ratio in must be whole numbers.

To simplify a ratio with parts:

Find the of the numbers in the ratio. This is the greatest factor that will divide into the numbers.
Divide each part by their HCF.

To simplify a ratio that includes decimal values:

Multiply the parts by the lowest power of ten to get whole number values. For example numbers with 1 place of decimals need to be multiplied by 10, numbers with 2 places of decimals need to be multiplied by 100
Divide each part by their HCF.

Examples

Skip image gallery

Image caption,
Simplify 10 : 8
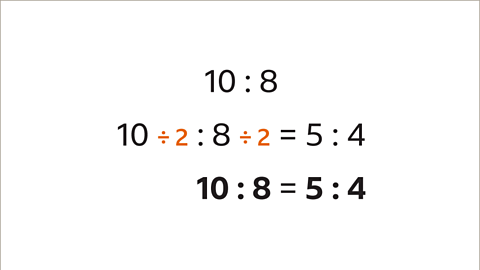
Image caption,
The HCF of 10 and 8 is 2. To simplify 10 : 8, divide each part (10 and 8) by their HCF (2). 10 : 8 simplifies to 5 : 4
Image caption,
Simplify 42 : 28 : 70
Image caption,
The HCF of 42, 28 and 70 is 14. To simplify 42 : 28 : 70, divide each part (42, 28 and 70) by their HCF (14). 42 : 28 : 70 simplifies to 3 : 2 : 5
Image caption,
Simplify 1∙5 : 6 : 2∙4
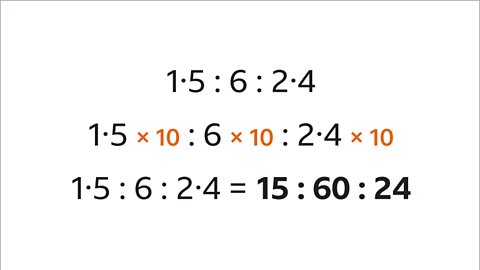
Image caption,
The ratio includes decimal values (1∙5 and 2∙4). Multiply all the parts (1∙5, 6 and 2∙4) by the lowest power of 10 that gives whole number values – in this example, this is 10. The equivalent ratio is 15 : 60 : 24. This ratio can be simplified.
Image caption,
The HCF of 15, 60 and 24 is 3. Divide the parts (15, 60 and 24) by their HCF (3). The simplified ratio is 5 : 20 : 8

Question

Simplify 3∙25 : 1∙5 : 4

Practise simplifying and writing equivalent ratios

Practise simplifying and writing equivalent ratios in this quiz. You may need a pen and paper to help you.

Quiz

Real-world maths

Image caption,
An artist will mix ratios of paint to get particular shades.

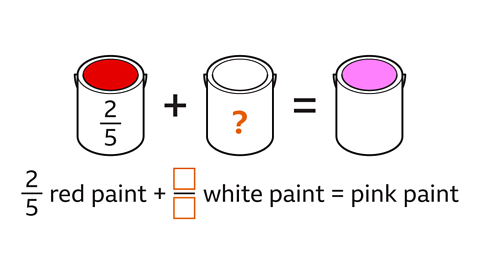
Ratios are used in any context that mixes parts together.

For example, an artist will mix colours on a palette to get particular shades.

Equal parts of the two primary colours red and yellow (a ratio of 1 : 1) give the secondary colour of orange.
A tertiary colour can then be mixed – this could be a red-orange or yellow-orange. The ratio of paint for these is 2 : 1, so:
- red-orange would be 2 parts red and 1 part yellow.
- yellow-orange would be 2 parts yellow and 1 part red.

Image caption,
An artist will mix ratios of paint to get particular shades.

Game - Divided Islands

More on Ratio

Find out more by working through a topic

Division in a given ratio
count
2 of 5
Solving ratio problems
count
3 of 5
Scale drawings
count
4 of 5
Map scales and ratio
count
5 of 5