Key points about algebraic reasoning and proof

Proof is a way to show a statement is always true by using worded or algebraic reasoning.
A counterexampleAn example to show a rule does not work all the time. can be used to show a statement is not always true.
Higher tier – There are algebraic ways to describe odd, even and consecutive integers, which are needed for some proofs.
Refresh your knowledge around this topic with this guide on expanding brackets and simplifying expressions.
Check your understanding
How to use algebra to demonstrate an argument
To argue mathematically, a statement must be backed up with evidence.
Examples can be used to demonstrate that rules are true for certain numbers. However, to prove a rule is true all the time, a clear, logical argument using words or algebra is needed.
Many proofs involve odd and even numbers. There are specific rules that apply:
| Adding | Multiplying |
|---|---|
| even + even = even | even × even = even |
| odd + odd = even | odd × odd = odd |
| even + odd = odd | even × odd = even |
| odd + even = odd | odd × even = even |
An example that disproves a rule is called a counterexampleAn example to show a rule does not work all the time.. Finding one counterexample is enough to disprove a rule.
An identityAn equation that is true no matter what values are chosen. The identity symbol ≡ links expressions that are identities. shows two expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms, eg 8 + 2, or 6𝑥, or 5𝑥² + 3𝑦, or 3𝑎𝑏𝑐. that are always equal.
Algebraic reasoning can be used to show that the left-hand side is the same as the right-hand side. This can involve expandExpanding means to multiply to remove the brackets., simplify (expression)To make an expression shorter by collecting terms of the same kind. or factoriseTo express a number or an expression as the product of its factors, eg 6 can be factorised as 2 × 3, and 6𝑛 – 12 can be factorised as 6(𝑛 – 2)..
Missing values can also be found by considering the termAn element within an algebraic sentence, eg 𝑥 or 5𝑦 or 3𝑒². on each side.
Follow the working out below
GCSE exam-style questions

- Show that 4(𝑥 − 2) + 6𝑥 + 10 ≡ 2(5𝑥 + 1).
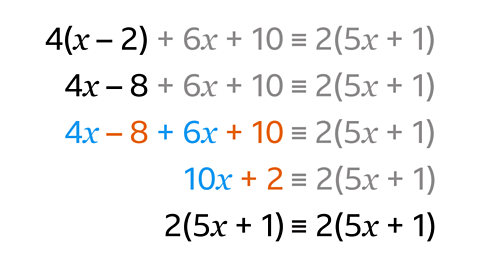
The identity symbol ≡ means 'is always equal to'.
The aim is to show that the left-hand side is equal to the right-hand side.
Start with the left-hand side.
Expand 4(𝑥 − 2) to get 4𝑥 − 8.
Simplify the left-hand side by collecting like terms.
4. Factorise the left-hand side to get 2(5𝑥 + 1).
The left-hand side and the right-hand side are the same, so the statement has been proven.
- Husnia says “𝑥² is always greater than 𝑥”.
Find a counterexample to show that Husnia is wrong.
The statement is not true when 𝑥 is \(\frac{1}{2} \).
Squaring means multiplying by itself.
Squaring \(\frac{1}{2} \) gives the answer \(\frac{1}{4} \).
\(\frac{1}{4} \) is less than \(\frac{1}{2} \).
\(\frac{1}{2} \) is a counterexample that shows Husnia is wrong.
Any fraction or decimal between 0 and 1 could be used as a counterexample to show the statement is not always true.
- If 𝑡 is odd, explain why 5𝑡 + 3 is even.
If 𝑡 is odd then 5𝑡 is also odd, because odd × odd = odd.
5𝑡 is odd and 3 is odd. Adding two odd terms together gives an even result.

Quiz - Algebraic reasoning
Practise what you've learned about algebraic reasoning with this quiz.
Higher - Proof
Video – Algebraic proof
Watch this video to work through example questions on algebraic proof for odd, even and consecutive integers.
Algebraic proof – Higher tier.
It is often helpful to use algebraic expressions to represent different types of numbers. 2𝑛, 6 times 𝑛 add 1, and 4𝑛 add 2 are all even algebraic expressions. This means that you can replace 𝑛 with any integer and you would get an even number.
Remember, integer just means a whole number, positive or negative.
Just like even numbers, these expressions have a factor of 2. Odd numbers are always 1 more or 1 less than even numbers. The same is true for algebraic expressions. Add or subtract 1 from an even expression and it is now odd. In fact, for any integer 𝑛, 2𝑛 can be used to represent any even number, and 2𝑛 add 1 represents any odd number.
These are called general expressions, and they are used in lots of algebraic proofs, which are statements that prove that something about a set of numbers is true.
Let's try a couple of questions.
Prove that the sum of three consecutive odd integers is always a multiple of 3.
Consecutive means numbers that are next to each other on a number line. For example, 1, 3, and 5 are three consecutive odd numbers. To get from one to the next, you add 2. This is true for all consecutive odd numbers. So, using the general expression for an odd number, 2𝑛 add 1, add 2 to get to the next one, 2𝑛 add 3, then add another 2 to get to the next, 2𝑛 add 5.
In algebraic proof questions, it's especially important to write down all your working out.
So, write ‘Let three consecutive odd numbers be 2𝑛 add 1, 2𝑛 add 3, add 2𝑛 add 5, where 𝑛 is any integer.’
Then, the question asks about their sum. So that's 2𝑛 add 1 add 2𝑛 add 3 add 2𝑛 add 5. Adding like terms gives 6𝑛 add 9.
Then, the question asks you to show this is a multiple of 3. 6𝑛 and 9 both have a factor of 3, so you can factorise this expression to 3 times 2𝑛 add 3. The multiplier 3 shows that it is always true that the sum of three consecutive odd integers is a multiple of 3.
The next question says: prove that the product of two consecutive even integers is always a multiple of 4.
Pause the video and have a go.
Before answering the question, let’s look at a number line. To get from one even number to the next, you add 2. So, start with the general expression for an even integer, 2𝑛, and then add 2 to get to the next consecutive even integer: 2𝑛 add 2.
Writing this formally, ‘Let two consecutive even numbers be 2𝑛 and 2𝑛 add 2, where 𝑛 is any integer.’
Product just means multiply by, so this is 2𝑛 multiplied by 2𝑛 add 2. 2𝑛 multiplied by 2𝑛 equals 4𝑛 squared and 2𝑛 multiplied by 2 equals 4𝑛, giving 4𝑛 squared add 4𝑛. This has a factor of 4, meaning it is a multiple of 4.
You should always finish a proof with a final statement: ‘So, it is always true that the product of two consecutive even integers is a multiple of 4.’
A mathematical proof is a sequence of statements that follow on logically from each other to show that something is always true.
Using letters to stand for numbers means that statements can be made about all numbers in general, rather than specific numbers.
Sometimes a proof may require certain types of integerIntegers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, –8, and 10,000 are examples of integers..
There are algebraic ways to describe odd and even integers, and consecutiveIntegers which follow on from each other continuously without gaps. For example, 1, 2, 3, 4, 5 and so on are consecutive numbers. 2, 4, 6, 8 are consecutive even numbers. integers that follow on from each other.
| Type of integers | Numerical examples | Algebraic examples |
|---|---|---|
| 3 different integers | 4, 7, 99 | 𝑛, 𝑚, 𝑝 |
| 3 consecutive integers | 4, 5, 6 | 𝑛, 𝑛 + 1, 𝑛 + 2 |
| 3 different even integers | 6, 8, 42 | 2𝑛, 2𝑚, 2𝑝 |
| 3 different odd integers | 9, 11, 37 | 2𝑛 + 1, 2𝑚 + 1, 2𝑝 + 1 |
| 3 consecutive even integers | 10, 12, 14 | 2𝑛, 2𝑛 + 2, 2𝑛 + 4 |
| 3 consecutive odd integers | 13, 15, 17 | 2𝑛 + 1, 2𝑛 + 3, 2𝑛 + 5 |
Follow the working out below
GCSE exam-style questions
- Prove that the sum of four consecutiveIntegers which follow on from each other continuously without gaps. For example, 1, 2, 3, 4, 5 and so on are consecutive numbers. 2, 4, 6, 8 are consecutive even numbers. odd numbers is always a multipleAn integer that is in the multiplication table of a specific number. For example, 20 is a multiple of ten because 20 is in the ten times table. of 8.
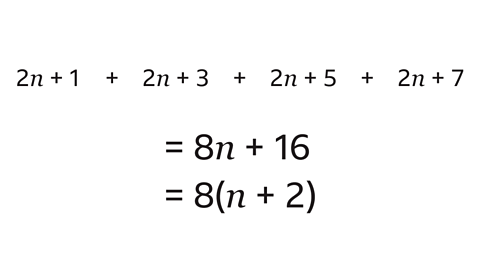
Write the first odd number as 2𝑛 + 1.
To find the next three odd numbers, add on 2 each time.
The next odd number is 2𝑛 + 3.
The next two consecutive odd numbers would be 2𝑛 + 5 and 2𝑛 + 7.
Add the four expressions by collecting terms. This gives 8𝑛 + 16.
To show this is a multiple of 8, factorise to take 8 out as a factor.
The expression has now been written as an integer (𝑛 + 2) multiplied by 8.
- Show that (3𝑛 + 2)² − (3𝑛 + 1)² ≡ 3(2𝑛 + 1)

For a ‘show that’ question, the left-hand side (LHS) of the identity needs to be shown to equal the right-hand side (RHS).
Start with the LHS. (3𝑛 + 2)² means (3𝑛 + 2) multiplied by itself.
Expand the brackets.
Simplify by collecting the 𝑛 terms in each section.
9n² − 6𝑛 − 1 is subtracted so each term here needs to be multiplied by −1.
Simplify by collecting like terms.
Factorise. The left-hand side of the identity is now shown to be the same as the right-hand side.
Higher - Quiz - Proof
Practise what you've learned about algebraic proof with this quiz for Higher tier.
Now you have revised algebraic reasoning and proof, why not try looking at inequalities?
More on Algebra
Find out more by working through a topic
- count4 of 14

- count5 of 14
- count6 of 14

- count7 of 14
