Challenge 5 - The Sculpture
Challenge 5 is all about shapes and working out areas.
Maths teacher Chris Smith and pupils from Grange Academy are here to explain.
The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.
Chris This problem is all about shapes and working out areas.
A sculpture consists of three large cubes stacked one on top of another without overhanging.
The edges of the largest cube measure 3 metres and its base is on the ground.
The next cube has edges 2 metres long and the top cube has edges that measure 1 metre.
The exposed surface has just been painted. Each tin of paint covered 10m squared.
How many tins of paint were needed?
Explain your answer.
Pupil: Think about how the sculpture looks from different viewpoints.
Pupil: Remember some parts won't need to be painted.
Pupil: You could try drawing the different sides or using blocks to help find the answer.
Pupil: Good luck!
So here's the challenge:
A sculpture consists of three large cubes stacked one on top of another without overhanging.
The edges of the largest cube measure 3 m and its base is on the ground.
The next cube has edges 2 m long.
The top cube has edges that measure 1 m.
The exposed surface has just been painted. Each tin of paint covered 10 m².
How many tins of paint were needed?
Need a hint?
Think about how the sculpture looks from different viewpoints.
Remember some parts won't need to be painted.
Try drawing the different sides or using blocks to help find the answer.
Solution
Worked out the answer? Here's how you can do it.
Did you work out how many tins of paint were needed?
Let’s look at how we got our answer.
There are four side views, each of which show a one-by-one square, on a two-by-two square on a three-by-three square.
One times one is one.
Two times two is four.
Three times three is nine.
Each side has an area of one plus four plus nine, which is 14 square metres.
Four times 14 equals 56 square metres.
Viewed from directly above, the sculpture will look like one large square.
The exposed top surfaces of the three cubes have the same area as one side of the largest cube, 3 metres by 3 metres, which is 9 square metres.
We can add the area of the top faces to the areas of the sides.
9 plus 56, gives a total surface area of 65 square metres.
Finally, tins of paint can cover ten square metres, so 65 divided by 10 gives us 6.5.
We need to round up to the nearest whole number, seven.
We needed seven tins of paint to cover the sculpture, and we had half a tin left over.
Great job if you had this one covered.
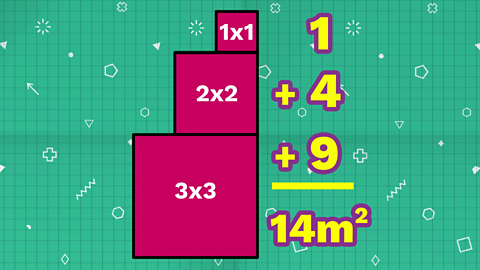
Step 1
Each side of the sculpture show a 1x1 square, on a 2x2 square on a 3x3 square.
1 x 1 = 12 x 2 = 43 x 3 = 9
Add these together to find the area of each side:
1 + 4 + 9 = 14
Each side has an area of 14 m².
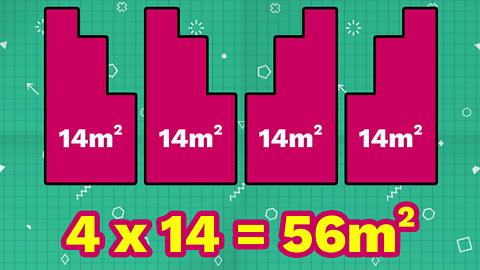
Step 2
Each of the four sides of the sculpture has the same area.
So we can find their total area by multiplying:
4 x 14 = 56m²
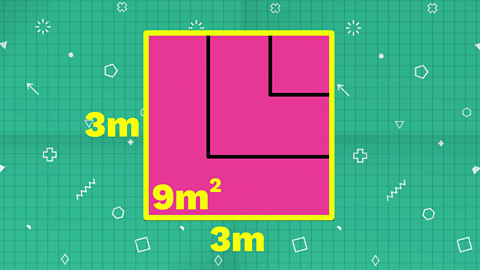
Step 3
Viewed from directly above, the sculpture looks like one large square.
The exposed top surfaces of the three cubes have the same area as one side of the largest cube:
3 x 3 = 9m²
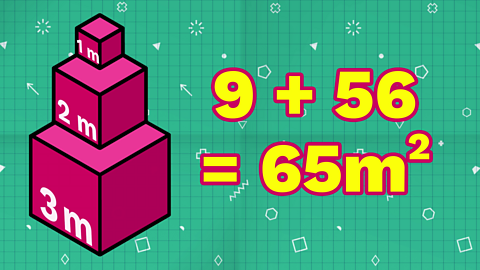
Step 4
We can add the area of the top faces to the areas of the sides.
9 + 56 = 65m²
The total surface area that needs to be painted is 65m²
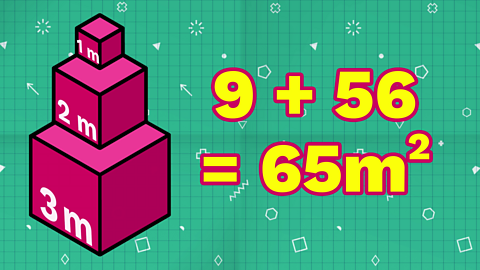
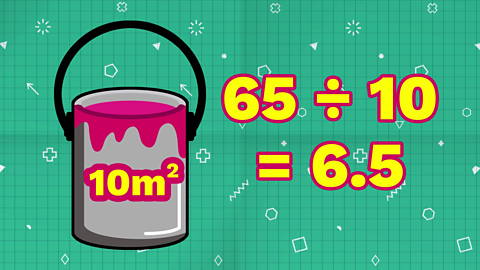
Step 5
Finally, tins of paint can cover ten square metres.
We can divide 65 by 10 to find out how many tins we need:
65 ÷ 10 = 6.5
No-one is going to sell you half a tin of paint, so we need to round up to the nearest whole number, seven.
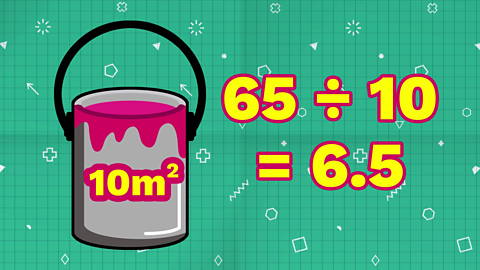
We needed seven tins of paint to cover the sculpture, and we had half a tin left over.
Maths Week Scotland 2023. list
Try out all the daily challenges from Maths Week Scotland 2023.
Maths Week Scotland 2022. list
Try out all the daily challenges from Maths Week Scotland 2022.
Maths Week Scotland 2021. list
Want more maths challenges? Here are all the problems from 2021.
More on Maths Week Scotland 2024
Find out more by working through a topic
- count1 of 8
