What are 2D shapes?
Two-dimensional (2D) shapes are completely flat. They cannot be picked up.
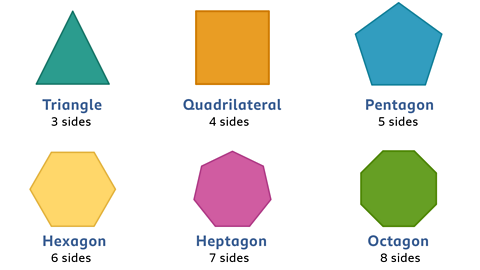
A polygon is a 2D shape with straight sides that meet at vertices.
Polygons have names that show the number of sides they have.
What are 3D shapes?
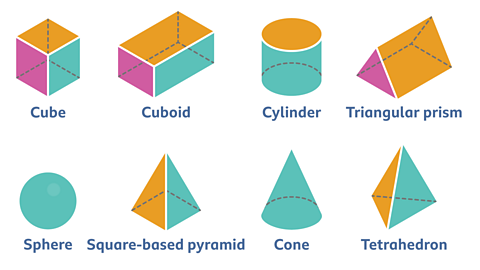
A three-dimensional (3D) shape is a solid shape.
3D shapes have three dimensions - length, width and depth.
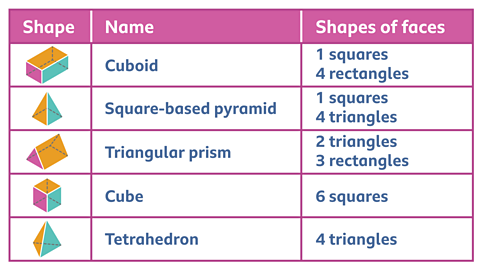
Look at the shapes of the faces to help recognise these 3D shapes.
3D shapes can have flat or curved faces.
Quiz: Sort 2D and 3D shapes
Why not see how much you know about this topic already? Then work through the page and see if you can beat your score.
Properties of polygons
Polygons have different properties that you can use to classify them. This includes:
- number of sides
- length of sides
- number of vertices
- size of the angles
Regular polygons are shapes where the lengths of the sides and the inside angles are equal.
Irregular polygons are shapes where the sides and inside angles are not equal.
Have a look at these two shapes. How are these the same? How are they different?

They both have four sides.
However, when you compare the properties, the length of the sides is the difference.
A square is a regular polygon. It has sides of equal length and equal angles.
A rectangle is an irregular polygon. It has equal angles, but the sides are not all equal in length.
Now look at these triangles. How are they the same? How are they different?

They all have the same number of sides and vertices.
However, look closely at the length of the sides and the angles.
Only the orange triangle has 3 equal sides and 3 equal angles.
This is a regular polygon. It is called an equilateral triangle.
The other triangles are irregular polygons.
Properties of 3D shapes
A 3D shape is a solid shape. 3D shapes have three dimensions:
- length
- width
- depth
3D shapes have different properties to 2D shapes.
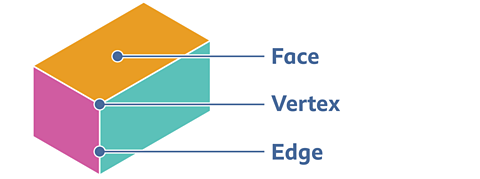
Faces - A face is a flat surface on a 3D shape.
Edges - An edge is where two faces meet. For example a cube has 12 edges.
Vertices - A vertex is a corner where edges meet. The plural is vertices.
For example, this cuboid above 6 faces, 12 edges and 8 vertices.
The table below shows how the faces of some other 3D shapes compare.
Sorting shapes
To sort shapes, you can compare different properties. Carroll diagrams and Venn diagrams can be used to sort shapes.

Image caption, Look at these 6 shapes. Let's sort them using a Carroll diagram and a Venn diagram
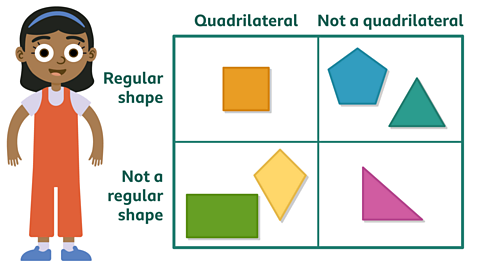
Image caption, Carroll diagram
A Carroll diagram is a table that can be used to group shapes according to their properties. Look at how these shapes have been sorted. Remember a quadrilateral is any shape with 4 straight sides.
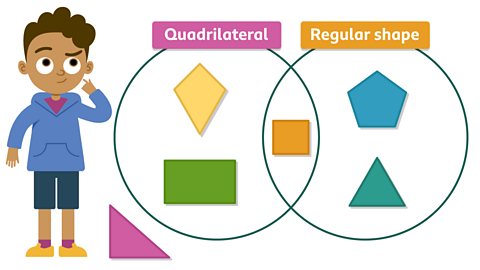
Image caption, Venn diagram
Now the shapes have been sorted using a Venn diagram. What is special about the square? It is a quadrilateral and a regular shape. Can you guess why the right-angled triangle in the outside set? It is not a quadrilateral or a regular shape.
1 of 3
Example 1
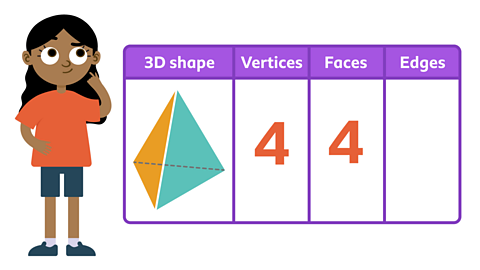
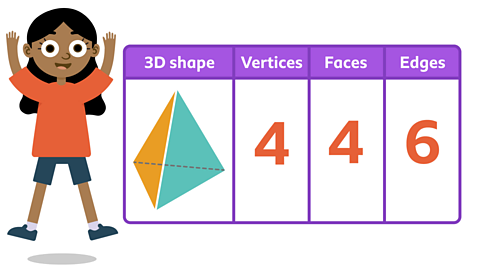
Maya needs help investigating the number of vertices, faces and edges of this shape.

Can you count the vertices and faces with her?
She is going to use a table to organise her findings.
✓ Maya counted 4 vertices and 4 faces. Did you get the same answer?
The 3D shape is a tetrahedron.
Example 2
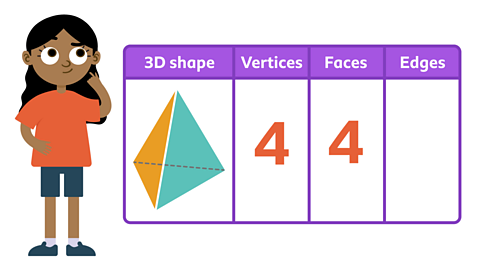
Maya thinks that 3D shapes always have the same number of edges as vertices.
Is she correct?
Count the number of edges to test her theory.
✓ Maya’s theory was incorrect.
The shape has 6 edges.
Remember, having ideas that turn out to be wrong is ok - this is why investigating is such an important part of maths!
Example 3
Did you notice that the tetrahedron had the same number of vertices as faces?
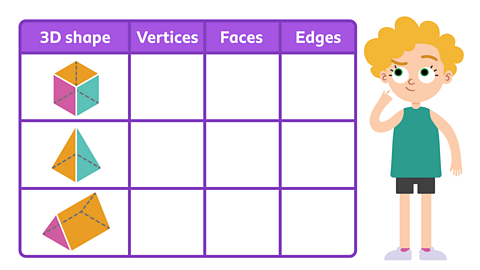
Do you think that all 3D shapes have the same number of vertices and faces?
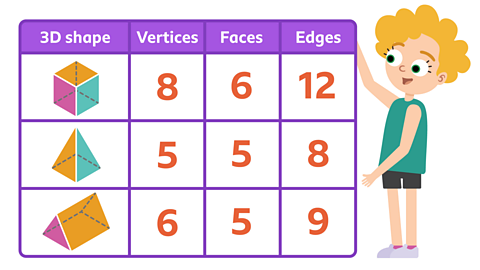
Test the theory - count the faces, vertices and edges of these 3D shapes.
✓ No, not all 3D shapes have the same number of vertices and faces.
Keep investigating! Look for patterns when you explore shapes and numbers.
More on 3D shapes
Find out more by working through a topic
- count2 of 4

- count3 of 4

- count4 of 4
