What are positive and negative numbers?
What are positive and negative numbers?
Any number above zero is a positive number.
Positive numbers are written with no sign or a '\({+}\)' sign in front of them and they are counted up from zero to the right on a number line.
Any number below zero is a negative number.
Negative numbers are always written with a '\({-}\)' sign in front of them and they are counted down from zero to the left on a number line.
Always look at the sign in front of a number to see if it is positive or negative.
Zero, \({0}\), is neither positive nor negative.
Key point
Positive numbers get higher the further we move right, so 5 is more than 2. Negative numbers get lower the further we move left, so -5 is less than -2.
Question
Which word, 'higher' or 'lower', would fit correctly in each of these gaps?
a) \({-7}\) is … than \({-1}\)
b) \({+62}\) is … than \({-71}\)
c) \({-136}\) is … than \({-36}\)
Answers
a) \({-7}\) is lower than \({-1}\)
b) \({+62}\) is higher than \({-71}\)
c) \({-136}\) is lower than \({-36}\)
Adding and subtracting positive and negative numbers
To add and subtract numbers always begin counting from zero.
When adding positive numbers, count to the right.
When subtracting positive numbers, count to the left.
Example
Calculate \(4 - 5 - 3\).
Imagine moving up and down a number line to get to the answer.
Starting from zero, count up to \({4}\).
Then subtract \({5}\).
Then subtract \({3}\).
\(4 - 5 - 3 = -4\).
The answer is \({-4}\).
Number line calculation
Image caption, Calculate 4 - 5 - 3

Image caption, Starting from zero, count up to 4.
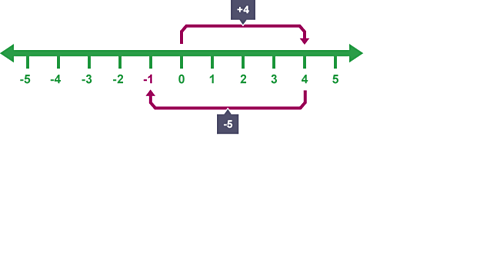
Image caption, Then subtract 5.
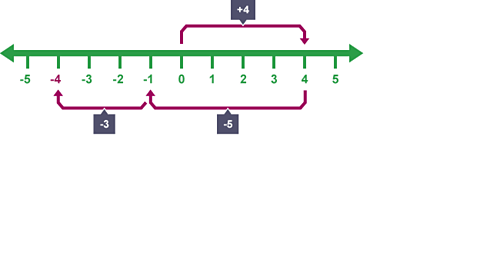
Image caption, Then subtract 3.
1 of 4
Question
Calculate: \(- 2 + 9 - 10 + 6\).
Answer
The answer is \({3}\) or \({+3}\).
Remember
- When adding positive numbers, count to the right.
- When adding negative numbers, count to the left.
- When subtracting positive numbers, count to the left.
- When subtracting negative numbers, count to the right.
Two signs side by side
- subtract when two different signs appear next to each other
- add when two of the same signs appear next to each other
Example
\(3 + {-5} = 3 - 5 = -2\)
\(3 - {-5} = 3 + 5 = +8\) (or \({8}\))
Question
Calculate:
a) \(10 + - 7\)
b) \(4 - - 3\)
Answer
a) \(10 + - 7 = 10 - 7 = 3\)
b) \(4 - -3 = 4 + 3 = 7\)
Multiplying and dividing positive and negative numbers
The rule for multiplying and dividing two numbers is very similar to the rule for adding and subtracting.
- When the signs are different the answer is negative.
- When the signs are the same the answer is positive.
Question
Calculate:
a) \(5 \times -4\)
b) \(-40 \div -8\)
Answer
a) We have \({+5}\) and \({-4}\).
The signs are different, so the answer will be negative.
So, \(+5 \times -4 = -20\)
b) We have \({-40}\) and \({-8}\).
The signs are the same, so the answer will be positive.
So, \(-40 \div -8 = 5\)
Making money add up: Positive and negative numbers
Work experience turns into a challenge for one girl as her boss asks her to complete the accounts. See how she uses positive and negative numbers to work it out.
No, Mrs Bradley, I can easily check if we haven’t gone overdrawn.
We did this in school, it was a cinch!
Oh no. Me? Complete an accounts review!
This is the worst work experience ever!
OK, calm down.
(RADIO PLAYS)
That’s better.
Now, tea.
So this is about money coming in and money going out, since last month.
That’s positive and negative numbers.
So first, let’s see what’s been paid into the bank.
Here are the paying in slips.
Now this can be Polly positive. Anything above zero is positive.
So I’ll stick the paying in slips on Polly.
This can be Nigella negative.
So I’ll stick all the receipts and money going out on Nigella.
Let’s imagine a line with a zero in the middle.
Everything you add on, adds to the right.
She told me that we started with a balance of £230 in the bank.
So that’s 230 positive.
So the paying in slips we’ll add on to the right.
Starting at 230 plus 1250.21 - that’s the takings from the first week of the month.
1480.21.
So let’s imagine that on my positive and negative line.
230 plus 1250.21 comes to 1480.21.
So I’ll just add up the remaining paying in slips and then add on to the right.
That was quick.
So the additional pay slips adding to the right comes to a total of 6313.41.
Now for the money going out.
I need all the receipts we’ve kept.
That will be negatives, subtracting.
While everything I add on, adds to the right.
Everything I subtract, subtracts to the left.
6313.41 minus £2600, that’s rent, minus £3000.20 that’s wages and then minus £840.09 for new hairdryers.
Woah. It’s gone negative?
OK that’s because I crossed the 0 line.
Let’s get my head round it.
Subtracting rent and wages brought us down to £713.21, then I took a further £840.09 away for the hairdryers.
The first £713.21 took me down to zero and the remainder took us down 126.88 to -126.88.
Oh no, we’ve still got one more payment to take out for the new chairs.
Oh dear, put it on Nigella.
So taking away another 721.50 equals -848.38.
So the -721.50 took us even further down to -848.38.
You can get to that figure by adding 126.88 and 721.50.
Wow, we’re bankrupt!
(PHONE RINGS)
Mrs. Bradley. Thank goodness!
What?
Refunds for the equipment we sent back?
So that’s money coming in in fact?
I’ll add in the five refunds.
Bye!
So let’s get my head round this.
Five payments of £240 were made last month that shouldn’t have been made.
I’m taking away these five lots of negatives. So I’m taking away five times the -240 and that’s going to add money in!
Oh I remember this.
A negative times a negative is a positive!
That’s what they said at school. In other words you can say.
When multiplying two signs that are the same, the answer is always positive.
Let’s check it.
5 x 240 = 1200.
-5 x -240 = 1200 as well, isn’t that clever!
Let’s get back to the line.
Starting at -848.38 we’re adding on 1200.
Well the first 848.38 takes us to zero.
We just have to work out the difference between 848.38 and 1200.
So we can find out how much to add on beyond zero.
Which is 1200 minus 848.38… equals 351.62.
There it is.
In the bank we have a credit of £351.62.
We’re rich!
Well I would be if she paid me anything.
Test section
Question 1
Which of these is the positive number?
\({5}\), \({-1}\) or \({0}\)
Answer
A positive number must have a \(+\) symbol in front of it or no symbol at all, and be a number higher than \({0}\).
So the answer is \({5}\)
Question 2
Is \({-36}\) is greater than \({-35}\)?
Answer
No.
\({-36}\) is less than \({-35}\).
Question 3
Calculate \({9}-{10}+{3}\).
Answer
\({9}-{10}={-1}\), \({-1}+{3}={2}\).
Question 4
Calculate \({-6}+{9}-{5}+{4}\).
Answer
\({-6}+{9}={3}\), \({3}-{5}={-2}\), \({-2}+{4}={2}\).
Question 5
Calculate \({15}+{-9}\).
Answer
When there are two different symbols next to each other, you need to subtract.
\({15}+{-9}={15}-{9}={6}\).
Question 6
Calculate \({6}-{-10}\).
Answer
You need to add when there are two of the same symbols next to each other.
\({6}-{-10}={6}+{10}={16}\).
Question 7
Calculate \({-8}\times{-3}\)
Answer
When multiplying, the answer will be positive if the symbols are the same.
\({-8}\times{-3}={24}\).
Question 8
Calculate \({-6}\times{9}\).
Answer
When multiplying, the answer will be negative if the symbols are different.\({-6}\times{9}={-54}\).
Question 9
Calculate \({-25}\div{-5}\).
Answer
When dividing, the answer will be positive if the symbols are the same. \({-25}\div{-5}={5}\)
Question 10
Calculate \({40}\div{-8}\)
Answer
When dividing, the answer will be negative if the symbols are different.
\({40}\div{-8}={-5}\).