Key points about order of operations and using negative numbers
- An acronym listing the order in which each part of a calculation must be worked out. Brackets, Indices (or pOwers), Division and Multiplication, and Addition and Subtraction. (or BODMAS) are acronyms that give the correct sequence of steps to process a calculation.
- A scientific calculator automatically uses the correct order of operations, a basic calculator does not.
- Use brackets when raising a A number less than zero. to a power on a calculator.
For this topic, be more confident by revising negative numbers and using a number line.
Video – Adding and subtracting with negative numbers
Watch the video to learn about adding and subtracting with negative numbers on a number line and by using number discs.
Adding and subtracting with negative numbers.
Let's talk about two ways to help add and subtract negative numbers.
First, number discs.
Each positive disc represents positive 1, or simply 1, and each negative disc represents negative 1. A positive and a negative disc added together form a zero pair. That's because they cancel each other out completely, to equal zero.
Let's look at some example questions:
To calculate negative 2 add 5, start with two negative discs, and then add five positive discs. There are two zero pairs that cancel each other out here, which leaves three positive discs. So, the answer is 3.
Alternatively, you can use a number line to work this out.
Find negative 2 on a number line and then move up five spaces to add 5. This gives the same answer, 3.
Let's try another question.
Work out negative 2 subtract 5.
Again, start with two negative discs. The question asks you to subtract 5, but notice that there aren't five positive discs to take away. But we can add five zero pairs. Notice that this doesn't change the total value of negative 2, because all the zero pairs are equal to zero, but this way gives us five new positive discs to subtract.
This leaves seven negative discs. So, the answer is negative 7.
We can work this out another way using discs.
To help, negative 2 subtract 5 is the same as negative 2 add negative 5.
So, we have two negative discs and then add in another five negative discs, which would mean we have seven negative discs in total.
Or, using the number line method, start at negative 2, and then move down five spaces to find the answer, negative 7.
The next question is 5 add negative 2.
Start with five positive discs, and then add two negative discs. This leaves two zero pairs to cancel, giving an answer of 3.
Using the number line method, adding a negative number is the same as subtracting a positive number. So, start at 5 and then move down two spaces to find the answer, 3.
Finally, let's try 5 subtract negative 2.
Why not pause the video and have a go at this one?
This is another case where you don't have the right discs to subtract. You need to subtract two negative discs, but you only have positive discs. So, add two zero pairs, and then subtract two negative discs, giving 7 as the solution.
Using a number line, subtracting a negative number is the same as adding a positive number. So, start at 5, and then move up two spaces to find the answer, 7.
What is the order of operations?
An acronym listing the order in which each part of a calculation must be worked out. Brackets, Indices (or pOwers), Division and Multiplication, and Addition and Subtraction. (or BODMAS) give the agreed order of operations in maths used to Work out the answer. For example, evaluate 2 + 3 means find the answer to 2 + 3. an A mathematical sentence expressed either numerically or symbolically made up of one or more terms, eg 8 + 2, or 6𝑥, or 5𝑥² + 3𝑦, or 3𝑎𝑏𝑐. :
- Brackets: Always work out the calculation in the brackets first. If there are brackets inside other brackets, work out the inside brackets first.
- Indices are pOwers: Such as 5\(^2\) or 2\(^3\).
- Division and Multiplication: Start on the left and work them out in the order that you find them.
- Addition and Subtraction: When only addition and subtraction are left in the calculation, work them out in order, starting from the left of the calculation and working towards the right.
Follow the working out below
GCSE exam-style questions
- Work out the value of this expression.
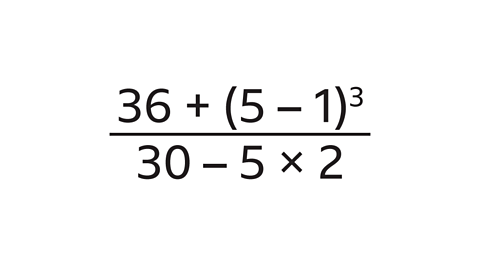
The value of the expression is 5.
The numerator and denominator are worked out separately then the division is calculated.
Calculate the numerator:
- The bracket is worked out first: 5 – 1 = 4
- Next the power (index) is calculated:
4\(^3\) is 4 cubed: 4 × 4 × 4 = 64 - Next the addition is worked out: 36 + 64 = 100
Calculate the denominator:
- The multiplication is worked out first: 5 × 2 = 10
- Next the subtraction: 30 – 10 = 20
- Finally, the numerator (100) is divided by the denominator (20):
100 ÷ 20 = 5
- Work out 20 – 3 × 4.
20 – 3 × 4 = 8
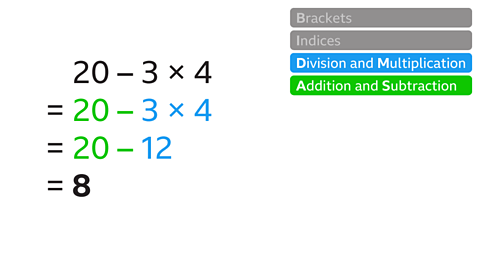
Use BIDMAS.
The order of operations means that the multiplication is worked out before the subtraction.
- Insert brackets in the statement 9 + 3 × 5 + 2, so that the answer is 30.
9 + 3 × (5 + 2) = 30
Without brackets the answer is: 9 + 3 × 5 + 2 = 26
- This is because the multiplication 3 × 5 is worked out before the addition.
To get the answer 30, one set of brackets is needed around the addition (5 + 2).
- Now the order of working is the bracket (5 + 2) = 7, then the multiplication, then the addition.
How to use a calculator
A scientific calculator works using A feature on a scientific calculator that makes it automatically follow the correct order of operations..
This means that a calculation can be entered as it is written, and the calculator will automatically use the correct order of operations.
Sometimes additional brackets are used for:
- Fraction calculations.
- Negative numbers.
- How many times to use the number in a multiplication. For example, 3² is 3 to the power 2 or 3 x 3 or 3 squared. of negative numbers.
Efficient use of a scientific calculator relies on understanding of the function keys, including the To enter a fraction on a calculator press the fraction button, enter the numerator, navigate down then enter the denominator., the Used to enter powers without multiplication, eg for 5⁶ enter: 5, power button, 6. and the Used on a calculator to move through a calculation. It can also be used to edit a calculation..
Remember
A basic calculator does not use DAL, so the calculation must be processed according to the rules of BIDMAS.
Follow the working out below
GCSE exam-style questions
- Work out the value of 𝑛\(^5\) – 𝑛 when 𝑛 = –2.
(–2)\(^5\) – (–2) = –30
Remember to use brackets when raising a negative number to a power.
→ open bracket (() → – 2 → close bracket ())
→ power button → 5
→ navigate right (►)
→ subtract (–)
→ open bracket (() → – 2 → close bracket ())
The display is (–2)\(^5\) – (–2)
→ equals (=)
- Use a calculator to work out the answer to this calculation.
Write down all the figures on your calculator display.
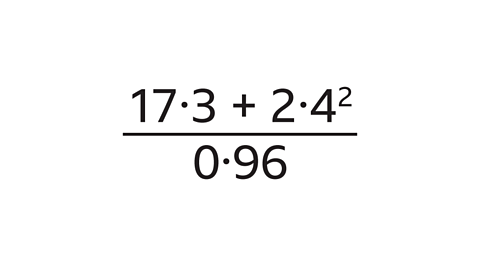
24·0208333333333333 or \(24.0208\dot{3}\)
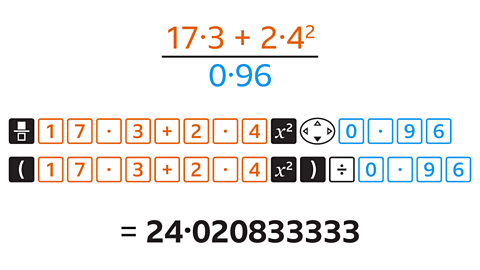
Enter the calculation by either using the fraction button:
→ fraction button → 17·3 → add (+) → 2·4
→ square button
→ navigate down (▼) → 0·96
→ equals (=)
Or by using brackets:
→ open bracket (() → 17·3 → add (+) → 2·4
→ square button
→ close bracket ()) → divide (÷) → 0·96
- Use your calculator to work out the answer to this calculation.
Write down all the figures on your calculator display.
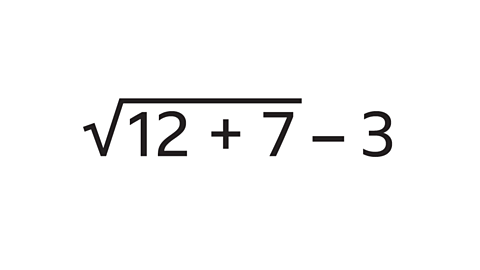
1∙358898944
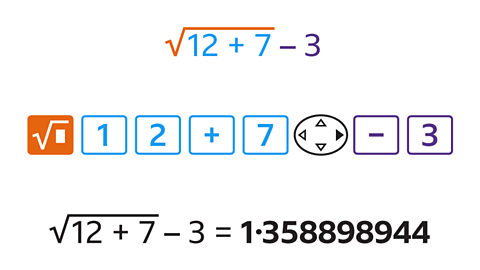
→ square root button → 12 → add (+) → 7
→ navigate right (►) → minus (–) → 3
→ equals (=)
Check your understanding
What are negative numbers?
A number less than zero. are written with a – sign in front.
A number line supports understanding of which numbers are larger or smaller.
- The further to the right from zero, positive numbers get larger.
- The further to the left from zero, negative numbers get smaller.
The symbol > is used when a value is greater than another, eg 23 > 5. The symbol < is used when a value is less than another, eg 11 < 40. are used to show which number is greater or smaller.
- –9 < –4 means that –9 is less than –4. The inequality points to the smaller value (–4).
- –4 > –9 means that –4 is greater than –9.
A number line may be drawn horizontally or vertically.
Revising using a number line will help with adding and subtracting negative numbers.
Follow the working out below
GCSE exam-style questions
- Order these negative numbers from smallest to largest:
–3 –0∙3 –13
From smallest to largest the numbers are: –13, –3, –0·3
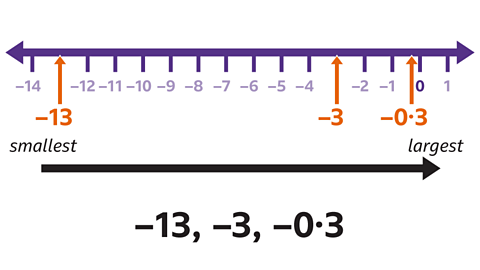
Smaller numbers are further to the left on the number line.
All negative numbers are to the left of zero on the number line.
- Which is greater?
–4 3
3 > –4
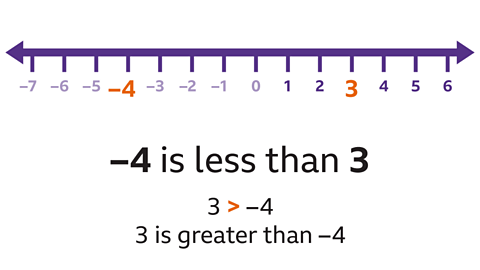
On a number line –4 is to the left of 3.
- –4 is less than 3.
- 3 is greater than –4.
This can be written with the > (greater than) The symbol > is used when a value is greater than another, eg 23 > 5. The symbol < is used when a value is less than another, eg 11 < 40..
How to add and subtract negative numbers
Adding using a number line
The first number is the starting point on the number line:
- To add a positive number, move to the right.
- To add a negative number, move to the left.
Subtracting using a number line
The first number is the starting point on the number line:
- To subtract a positive number, move to the left.
- To subtract a negative number, move to the right.
Remember
Adding a negative number is the same as subtracting a positive number.
Subtracting a negative number is the same as adding a positive number.
Follow the working out below
GCSE exam-style questions
- Work out –5 + 11.
–5 + 11 = 6
- The first number (–5) is the starting point on the number line.
- To add a positive number move right on the number line.
- Move 11 places to the right.
- Work out –19 – –24.
The answer is 5.
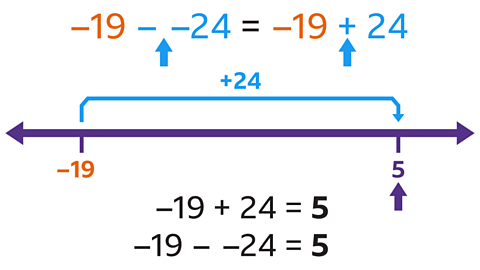
Subtracting a negative number is the same as adding a positive number:
- –19 – –24 is the same as –19 + 24, both = 5.
This can also be worked out using a number line as a guide:
- The first number is the starting point –19.
- To subtract a negative number move right on the number line.
- – –24 means move 24 places right.
- –19 – –24 = 5
When multiplying and dividing negative numbers, it is useful to complete the calculation initially using positive numbers.
Follow the working out below
GCSE exam-style questions
- Work out the answer to –20 × 5.
–20 × 5 = –100
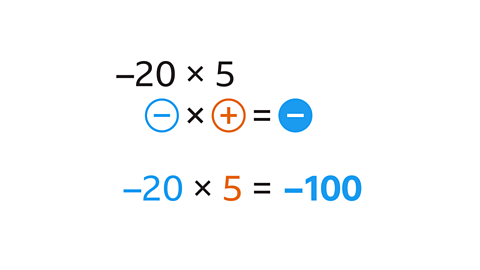
The two numbers have different signs, so the answer will be negative.
- Work out the answer to –3 × 12 ÷ –2.
–3 × 12 ÷ –2 = 18
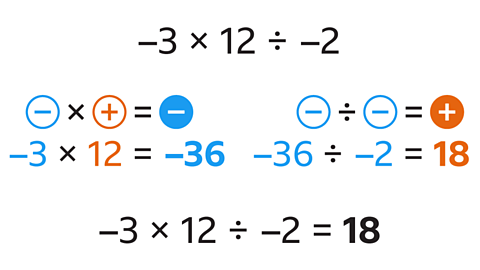
The first two numbers have different signs, so the answer will be negative:
–3 × 12 = –36
In the next calculation the numbers have the same signs, so the answer will be positive:
–36 ÷ –2 = 18
Quiz - Order of operations and negative numbers
Practise what you've learned about order of operations and negative numbers with this quiz. The questions change each time you try, so keep testing your knowledge.
Now you've revised order of operations and using negative numbers, why not try learning about adding, subtracting, multiplying and dividing fractions?
More on Number
Find out more by working through a topic
- count3 of 15
- count5 of 15
- count6 of 15
