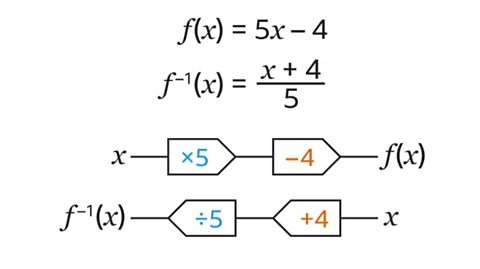
Key points about simplifying expressions and expanding brackets

- To simplify an expressionAn expression is a set of terms combined using the operations +, –, 𝑥 or ÷. For example 5𝑥2 – 3𝑥𝑦 + 17. An expression does not have an equals sign., group term (algebra)An element within an algebraic sentence, eg 𝑥 or 5𝑦 or 3𝑒². Elements (terms) are separated by + or – signs. together by collecting, multiplying or dividing like terms.
- To expand an expression that contains one bracket, multiply everything inside the bracket by the letter or number outside the bracket.
- To expand an expression containing two brackets, multiply every term in the first bracket by every term in the second bracket.
Refresh your knowledge on the order of operations and negative numbers to help with your understanding of algebra.
Video – Expanding double brackets
Watch this video to see how to expand double brackets using the grid or FOIL method.
Expanding double brackets.
Let's look at two different methods for expanding double brackets.
Question 1 asks you to expand the brackets 2𝑥 add 8 multiplied by 𝑥 subtract 3. Let's use the grid method for this one.
In a grid like this, write the terms from one bracket in the top row and the terms from the otherbracket down the left-hand column. Then, fill in the middle boxes by multiplying each term from the top row with each term from the left-hand column. 2𝑥 multiplied by 𝑥 equals 2𝑥 squared, 2𝑥 multiplied by –3 equals –6, 8 multiplied by 𝑥 equals 8𝑥, and 8 multiplied by –3 equals -24.
Then, adding these values together gives the expansion of this set of brackets: 2𝑥 squared add 8𝑥 subtract 6𝑥 subtract 24. Finally, simplify where you can. 8 and –6𝑥 are both terms in 𝑥, so they can be simplified. Be careful with negative numbers here. 8𝑥 subtract 6𝑥 equals 2𝑥. So, the final answer is 2𝑥 squared add 2𝑥 subtract 24.
OK. Let's look at another question: expand the brackets 𝑥 add 2 multiplied by 𝑥 subtract 5. Let's use the FOIL method for this one. FOIL stands for: First, Outer, Inner, and Last. This gives you an order for multiplying the terms in the first bracket by those in the second bracket.
So, start by multiplying the first term in each bracket: 𝑥 multiplied by 𝑥 equals 𝑥 squared. Next, multiply the two outer terms, which are the terms on the outside of the expression: 𝑥 multiplied by –5 equals –5𝑥. Then multiply the two inner terms. These are the two on the inside of the expression. 2 multiplied by 𝑥 equals 2𝑥. Finally, multiply the last term in each bracket. These are 2 and –5, which multiply to give –10.
Always remember to simplify your answer by collecting like terms. –5𝑥 and 2𝑥 are both 𝑥 terms. So they can be simplified to give –3𝑥. This gives a final answer of 𝑥 squared subtract 3𝑥 subtract 10.
Either the grid method or FOIL can be used to expand double brackets, so choose the one you're most confident with when answering these types of questions.
Algebraic definitions
| Key term | Definition |
|---|---|
| Variable | A letter that represents an unknown value. The letters 𝑥 or 𝑦 are often used as variables. The value of a variable can change. |
| Term | A number or letter on its own, or numbers and letters multiplied together, such as −2, 3𝑥 or 5𝑎². |
| Expression | One or more terms combined using the operations +, –, × or ÷. For example −4𝑥 − 3 or 5𝑥² – 3𝑥𝑦 + 17. An expression does not have an equals sign. |
| Equation | An equation states that two expressions are equal in value, and contains an equals sign. For example 4𝑏 − 2 = 6. An equation is only true for certain values. |
| Identity | A statement that is true no matter what values are chosen, for example 4𝑎 × 𝑎² ≡ 4𝑎³. The triple equals sign (≡) means ‘is always equal to’. |
| Formula | A rule that links two or more variables. For example 𝑣 = 𝑢 + 𝑎𝑡. |
Writing expressions
Statements can be written as expressionAn expression is a set of terms combined using the operations +, –, 𝑥 or ÷. For example 5𝑥2 – 3𝑥𝑦 + 17. An expression does not have an equals sign. using algebra.
Follow the working out below
GCSE exam-style questions
- John is 𝑛 years old.
Kim is three years younger than John.
Vanessa is half Kim's age.
Write an expression for each person's age.
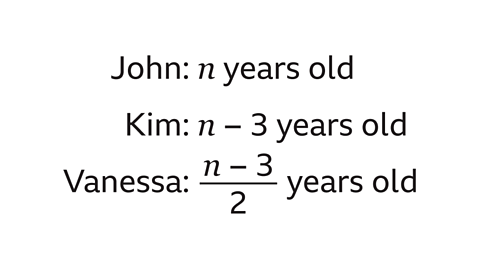
Kim is three years younger than John, so Kim is 𝑛 − 3 years old.
Vanessa is half Kim's age, so take Kim's age and divide by 2.
This gives Vanessa's age as \(\frac{(𝑛 -3)}{2}\).
- The number of oranges Naledi has is 𝑏 and the number of grapes she has is 𝑐. The number of oranges she has is half the number of grapes.
Which of these statements is correct: 𝑐 = 2𝑏 or 𝑏 = 2𝑐?
𝑏 = 2𝑐
The number of grapes, 𝑏, is twice the number of oranges, 𝑐.
Check the answer with an example:
Suppose Naledi has 12 grapes, so 𝑏 = 12.
She has half as many oranges as she has grapes, so 𝑐 = 6.
In this example, when 𝑐 = 6, 𝑏 = 12. 𝑏 is twice as much as 𝑐.
We can write this as an equation: 𝑏 = 2𝑐.
Simplifying expressions
Expressions where terms are added or subtracted can be simplified by collecting term (algebra)An element within an algebraic sentence, eg 𝑥 or 5𝑦 or 3𝑒². Elements (terms) are separated by + or – signs. that contain the same variableAn unknown value, usually represented by a letter such as 𝑥 or 𝑦. . These terms are called 'like terms.'
In the expression 5𝑎 + 2𝑏² + 3𝑎 − 6𝑏 + 𝑏², the terms 5𝑎 and +3𝑎 are like terms. 2𝑏² and 𝑏² are also like terms. −6𝑏 does not have a like term.
Expressions where terms are multiplied or divided can sometimes be simplified by using indicesIndices are powers. For example, 3 to the power of 2, written 3². The singular for indices is 'index'..
𝑎² × 𝑎³ means 𝑎 × 𝑎 × 𝑎 × 𝑎 × 𝑎, which is written as 𝑎⁵.
When multiplying terms with indices, add the powers.𝑎⁵ ÷ 𝑎³ = 𝑎².
When dividing terms with indices, subtract the powers.
Follow the working out below
GCSE exam-style questions
- Simplify 2𝑥 – 4𝑦 + 1 – 3𝑥 + 7𝑦 – 4.
− 𝑥 + 3𝑦 – 3
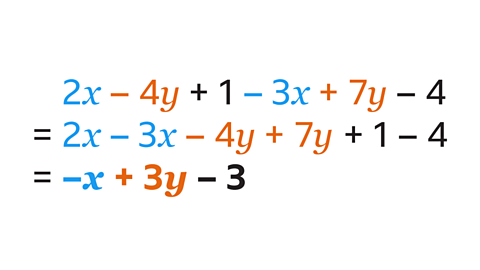
Collect the like terms:
- 2𝑥 − 3𝑥 = −𝑥
- − 4𝑦 + 7𝑦 = 3𝑦
- +1 – 4 = –3
- Simplify 3𝑎𝑏²𝑐³ × 4𝑎²𝑏³𝑐⁴.
12𝑎³𝑏⁵𝑐⁷
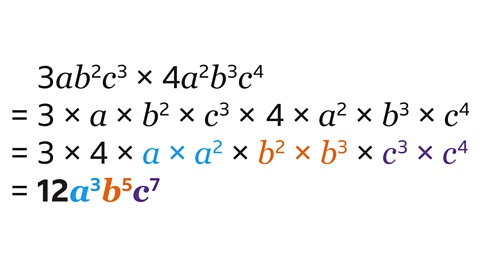
Multiply all the terms that involve the same letter by adding the indices.
For example, 𝑏² x 𝑏³ = 𝑏 x 𝑏 x 𝑏 x 𝑏 x 𝑏 = 𝑏⁵
Expanding a single bracket
Expanding a brackets means multiplying everything inside the bracket by the letter or number outside the bracket.
For example, to expandExpanding a brackets means multiplying everything inside the bracket by the letter or number outside the bracket to remove the brackets, eg 3(𝑚 + 7) = 3 × 𝑚 + 3 × 7 = 3𝑚 + 21. the expressionAn expression is a set of terms combined using the operations +, –, 𝑥 or ÷. For example 5𝑥2 – 3𝑥𝑦 + 17. An expression does not have an equals sign. 3(𝑚 + 7), both 𝑚 and 7 must be multiplied by 3:
3(𝑚 + 7) = 3 × 𝑚 + 3 × 7 = 3𝑚 + 21.
The process of expanding does not change the value of the expression. This means that 3(𝑚 + 7) and 3𝑚 + 21 are equivalentsThe same as but in a different form, eg ½ is equivalent to 50%. to each other.
Expanding brackets uses the skills of simplifying algebra.
Follow the working out below
GCSE exam-style questions

- Expand 5𝑝³𝑞(4𝑝𝑞 – 2𝑝²𝑞³).
20𝑝⁴𝑞² – 10𝑝⁵𝑞⁴
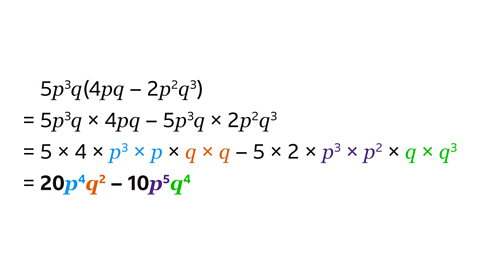
- Multiply both terms in the bracket by 5𝑝³𝑞.
- Simplify the two expressions.
- Remember to add the powers when multiplying terms with indices.
- Expand and simplify 8𝑔 + 2𝑔(3𝑔 + 7).
6𝑔² + 22𝑔
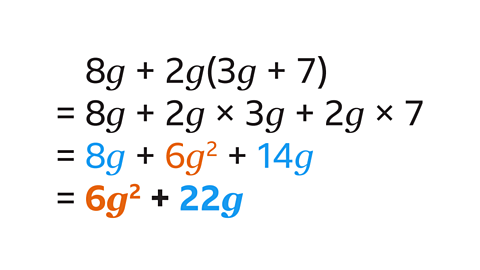
- Remember to use the correct order of operations.
- Expand the bracket first:
- 2𝑔(3𝑔 + 7) = 6𝑔² + 14𝑔
- Add like terms. 8𝑔 and 14𝑔 are like terms so can be added to give 22𝑔.
- Expand and simplify 3(2𝑐 + 5) – 4(𝑐 + 5).
2c + 35
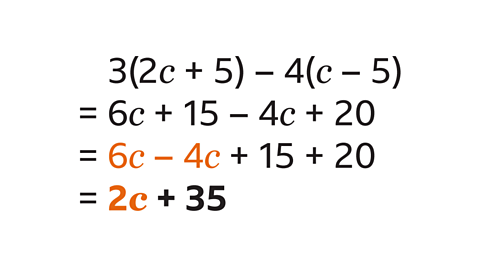
- Expand the first bracket:
- 3(2c + 5) = 6c + 15
- Expand the second bracket. Remember –4 × –5 = 20:
- 4(c – 5) = – 4c + 20
- Collect like terms:
- 6c – 4c = 2c
- 15 + 20 = 35
Expanding double brackets
Writing two brackets next to each other means the brackets need to be multiplied together.
For example (𝑦 + 2)(𝑦 + 3) means (𝑦 + 2) × (𝑦 + 3).
When expanding double brackets, every term in the first bracket has to be multiplied by every term in the second bracket.
Follow the working out below
GCSE exam-style questions
- Expand (3𝑥 – 2)(2𝑥 – 4).
6𝑥² – 16𝑥 + 8
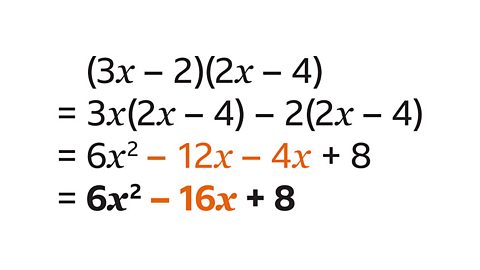
- Multiply every term in the first bracket by every term in the second bracket.
- Remember 3𝑥 × 2𝑥 means 3 × 𝑥 × 2 × 𝑥.
- 3𝑥 × 2𝑥 = 6𝑥²
- –2 × –4 = 8
- Simplify the like terms –12𝑥 and –4𝑥 to get –16𝑥.
- Expand (3𝑥 – 2)(2𝑥 + 1).
6𝑥² – 𝑥 – 2
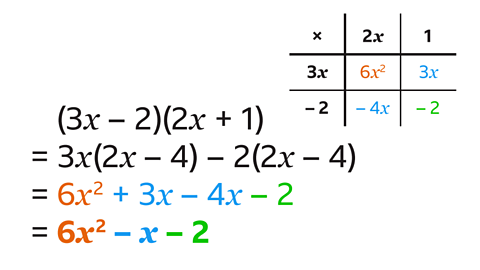
- If using a grid, write the terms from the brackets on the side and top.
- Fill in the inside of the grid by multiplying the terms together.
- Add the four terms together and collect the like terms.
Quiz - Expanding brackets
Practise what you've learned about simplifying expressions and expanding brackets with this quiz.
Higher - How to expand three brackets
To expand three brackets, first expand and simplify two of the brackets, then multiply the result by the remaining bracket.
Follow the working out below
GCSE exam-style questions

Expand (𝑥 – 2)(𝑥 + 6)(𝑥 – 3).
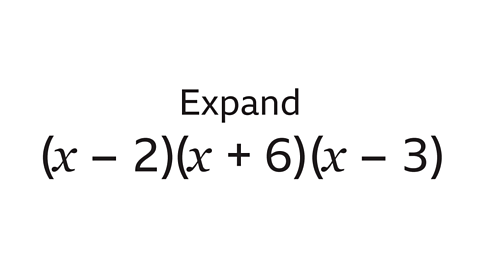
𝑥² + 𝑥³ – 24𝑥 + 36
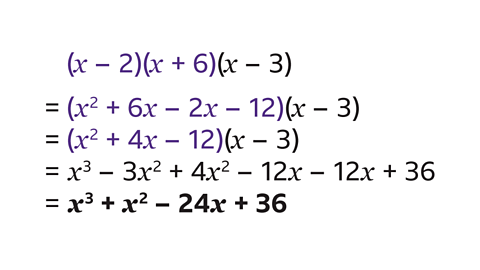
- Expand the first two brackets:
- (𝑥 – 2)(𝑥 + 6) = 𝑥² + 6𝑥 – 2𝑥 – 12.
Collect like terms to give 𝑥² + 4𝑥 – 12.
Multiply 𝑥² + 4𝑥 – 12 by 𝑥 – 3. Multiply every term in the first bracket by every term in the second bracket.
Collect like terms to give the simplified answer.
Higher - Quiz - Expanding three brackets
Practise what you've learned about simplifying expressions and expanding three brackets with this quiz.
Now you've revised simplifying expressions and expanding brackets, why not look at algebraic reasoning and proof?
More on Algebra
Find out more by working through a topic
- count2 of 14

- count3 of 14
- count4 of 14

- count5 of 14