Key points about functions
- A function, 𝑓(𝑥), is a type of A mathematical rule that links variables, by substituting the values that can be changed with words or letters, eg 𝑎² + 𝑏² = 𝑐². A formula contains an equals (=) sign. that links an input with an output.
- The The opposite of a mathematical process. For example, the inverse of × 5 is ÷ 5. The inverse process undoes the original process. function, 𝑓\(^-\)\(^1\)(𝑥), is found by changing the The subject of a formula or equation is the variable on its own on one side of the equals sign, eg 𝑦 is the subject in 𝑦 = 3𝑥 + 5..
- A Where the output of one function is used as the input of another for two functions. 𝑔𝑓(𝑥) is a composite function where the output of 𝑓(𝑥) is used as the input of the function 𝑔., such as 𝑔𝑓(𝑥) is a function of a function.
Support your confidence in this topic by refreshing your knowledge of substitution and changing the subject of formulae.
Check your understanding
Function notation
A function takes an input value, applies a rule to it, and produces an output value.
This can be demonstrated using a function machine.
The function, multiply by 3 and then subtract 1, can be applied to different values. If 5 is the input, the output is 14 because 5 × 3 – 1 = 14.
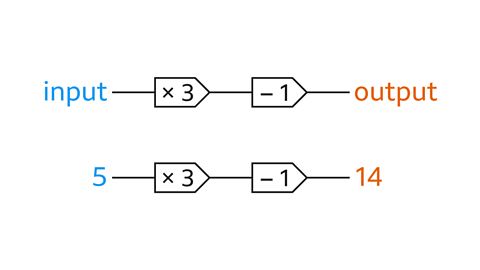
For instance, for the function 𝑓(𝑥) = 3𝑥 – 1, 𝑥 is the input and 𝑓 is the function that we apply, which in this example is 3𝑥 – 1.
𝑓(𝑥) is said aloud as '𝑓 of 𝑥'.
Follow the working out below
Inverse functions
An inverse function links the output value back to the input value, meaning it is the original function in reverse.
An inverse function is written as 𝑓\(^-\)\(^1\)(𝑥).
The inverse function of 𝑓(𝑥) is said aloud as 'inverse 𝑓 of 𝑥'.
To find an inverse function, the equation is rearranged to change the subject and use inverse processes.
For example, for a function that multiplies by 3 and subtracts one, the inverse function is add one and then divide by 3.
A function machine can help you to check your steps are in the correct order:
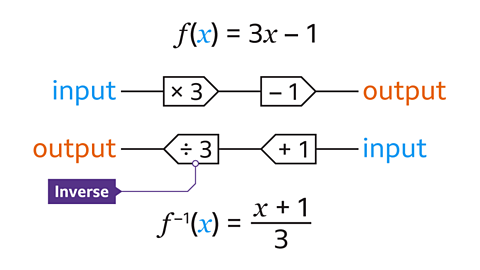
Follow the working out below
GCSE exam-style questions
- 𝑓(𝑥) = 3𝑥² + 7
Find the inverse function, 𝑓\(^-\)\(^1\)(𝑥).
\((x) =\sqrt{\frac{x – 7}{3}}\)
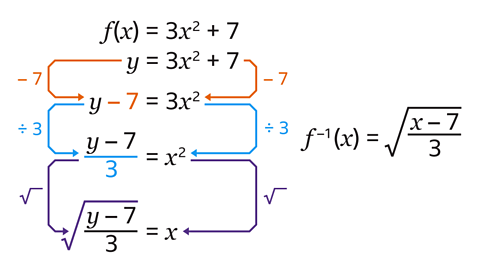
- Replace 𝑓(𝑥) with 𝑦.
- Rearrange to make 𝑥 the subject. Take care when choosing inverse operations and use order of operations (BIDMAS) in reverse. When square rooting both sides, the square root goes over the whole expression.
- Replace the 𝑦 with 𝑥.
- Label the expression as 𝑓\(^-\)\(^1\)(𝑥).
- 𝑓(𝑥) = \(\frac{𝑥}{6}\)
Find 𝑓\(^-\)\(^1\)(–3).
𝑓\(^-\)\(^1\)(–3) = 18
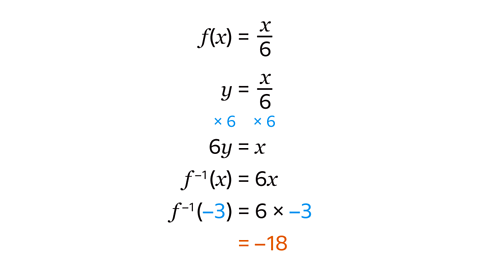
- First, find the inverse function.
- Replace 𝑓(𝑥) with 𝑦.
- Rearrange to make 𝑥 the subject.
- Replace the 𝑦 with 𝑥.
- Write the expression containing x equal to 𝑓\(^-\)\(^1\)(𝑥).
- The inverse function is 𝑓\(^-\)\(^1\)(𝑥) = 6𝑥.
- Substitute –3 in place of 𝑥 to reach the answer of –18.
Composite functions
Where the output of one function is used as the input of another for two functions. 𝑔𝑓(𝑥) is a composite function where the output of 𝑓(𝑥) is used as the input of the function 𝑔. are created by combining two functions. They are made when the output from one function is used as the input for another function.
If there are two functions listed, they are usually named 𝑓 and 𝑔.
The composite function 𝑓𝑔(𝑥) is said as '𝑓 of 𝑔 of 𝑥'.
𝑓𝑔(𝑥) is calculated by finding 𝑔(𝑥) first, and then In algebra, to replace a letter with a number. this into the function 𝑓.
So, 𝑓𝑔(𝑥) = 𝑓[𝑔(𝑥)].
Follow the working out below
GCSE exam-style questions
- 𝑓(𝑥) = 𝑥 – 7 and 𝑔(𝑥) = 3𝑥 + 1
Find 𝑔𝑓(5).
𝑔𝑓(5) = –5
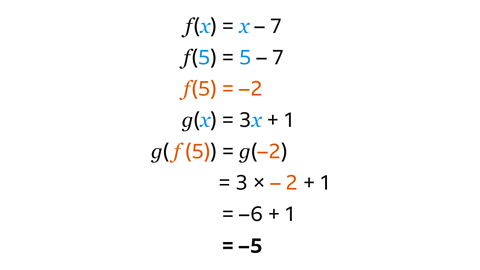
- 𝑔𝑓(5) means 𝑔[𝑓(5)].
- Find 𝑓(5) first.
- Input 5 into the function 𝑓.
- The function 𝑓 says to subtract 7.
- 𝑓(5) = –2.
- Input the value of 𝑓(5) into the function 𝑔.
- The function 𝑔 says to multiply by 3, then add 1.
- 𝑔(–2) = –5
- 𝑓(𝑥) = 5𝑥 and 𝑔(𝑥) = 𝑥² + 3
Find 𝑔𝑓(𝑥).
𝑔𝑓(𝑥) = 25𝑥² + 3
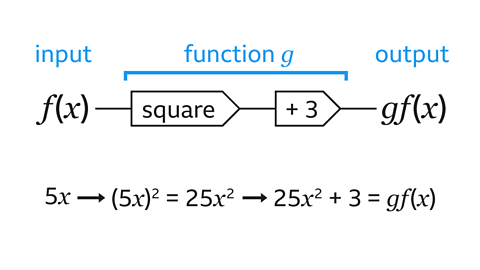
- 𝑔𝑓(𝑥) means to input 𝑓(𝑥) into the function 𝑔.
- The function 𝑔 says to square the input then add 3.
- 𝑓(𝑥) is 5𝑥.
- Squaring 5𝑥 means 5𝑥 × 5𝑥, which is 25𝑥².
- 𝑔𝑓(𝑥) = 25𝑥² + 3.
- 𝑓(𝑥) = 3𝑥 + 2 and 𝑔(𝑥) = 𝑥 – 6
Solve 𝑓𝑔(𝑥) = 14.
𝑥 = 10
![fg(x)=f[g(x)]=3(x-6)+2. =3x-18+2. =3x-16. 3x-16=14. 3x=30. x=10.](https://ichef.bbci.co.uk/images/ic/480xn/p0jyflyp.png)
- 𝑓𝑔(𝑥) means to perform the function 𝑓 with 𝑔(𝑥) as the input.
- The function 𝑓 says to multiply by 3, then add 2.
- Multiply 𝑥 – 6 by 3, and then add 2.
- Expand and simplify to get a simplified version of 𝑓𝑔(𝑥).
- Finally put this expression equal to 14 and solve.
Higher – Quiz – Functions
Practise what you've learned about functions with this quiz for Higher tier.
Now that you've revised higher functions, why not take a look at algebraic reasoning and proof?
More on Algebra
Find out more by working through a topic
- count6 of 14
- count7 of 14
- count8 of 14
- count9 of 14
