Key points about decimals

- Each digit of a number has a place valueThe value of a digit that relates to its position or place in a number, eg in 1482 the digits represent 1 thousand, 4 hundreds, 8 tens and 2 ones., which are all power of tenThe power of ten tells us how many times to use the number in a multiplication. For example 10² means 10 × 10 = 100. Powers of ten are 10, 100, 1000 and so on. .
- The decimal point separates the whole numbers from the parts (or fractions) of a number.
- The process for decimal arithmetic uses the same methods as whole numbers.
Understanding place value is essential for ordering decimals.
Video – Dividing by decimals
Watch this video to learn how to use equivalent fractions to divide numbers by decimals.
Dividing by decimals.
The fractions one half, two quarters, and four eighths are all equivalent, or equal, to each other.
To understand this better, imagine slicing a pizza into two equal parts. One part equals one half of the pizza. If you slice the same pizza into four equal parts, two parts equal two quarters of the pizza. The amount of pizza in each diagram is the same because one half also equals two quarters.
Understanding equivalent fractions makes dividing by decimals easier.
For example, to simplify 3 divided by 0.6, multiply both the dividend, which is the numerator, and the divisor, which is the denominator, by 10. 3 multiplied by 10 equals 30, and 0.6 multiplied by 10 equals 6. This gives 30 over 6. This is now an equivalent fraction with a whole number divisor, which is easier to work with than a decimal divisor.
Always remember to simplify your answer as much as possible: 30 divided by 6 equals 5, and so 3 divided by 0.6 also equals 5.
Let's look at an example question:
Mila is pouring 2 litres of orange juice into cups. Each cup holds 0.5 litres. Work out how many cups she can fill.
To work this out, divide 2 litres by 0.5, so 2 over 0.5. Start by changing the denominator, 0.5, into a whole number by multiplying by 10. That makes the denominator 5. And remember to multiply the numerator by 10 too.
This gives an equivalent fraction of 20 divided by 5, which equals 4. So, Mila can fill four 0.5-litre cups.
What if Mila has 0.96 litres of orange juice and cups that hold 0.06 litres?
This means 0.96 divided by 0.06. 0.06 has 2 decimal places. So, this time, multiply 0.06 by 100 to get a whole number, which is 6. Then, multiply 0.96 by 100 too, to get the equivalent fraction: 96 over 6.
You can use short division to show that 6 goes into 9 one time with 3 remaining, and 6 goes into 36 six times, with zero remaining.
So, the answer is 16 cups.
How to use place value to order decimals
The decimal point of a whole number comes after the last digit.
To compare a list of decimal numbers:
- List the numbers, one on top of the other, lining up the decimal points to get each digit in the correct column.
- If the numbers have a different amount of digits, there may be some gaps in the columns. Fill any gaps with a zero.
- Compare the digits in the columns, starting at the left with the greatest place value.
- If digits are equal in a column, move to the next column to the right and compare those digits.
Once each number is compared, they can be put in ascendingArranged from least value to greatest value, eg 1, 2, 3. or descendingArranged from greatest value to least value, eg 3, 2, 1. order.
inequality symbols (< >)The symbol > is used when a value is greater than another, eg 23 > 5. The symbol < is used when a value is less than another, eg 11 < 40. can be used to state whether one value is less than (<) or greater than (>) another.
Following the working out below
GCSE exam-style questions
- Write these numbers in order from smallest to largest:
0·3, 0·33, 0·303, 0·033.
0·033, 0·3, 0·303, 0·33.
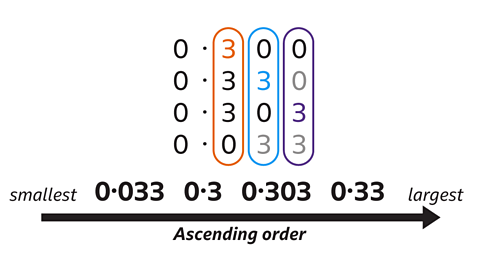
- List the numbers, on top of each other, lining up the decimal points.
- Write in additional zeros so all the numbers have the same number of decimal places (3).
- Compare the digits one column at a time, working from left to right.
- Which number is greater:
0·909 or 0·0999?
0·909 is greater than 0·0999.
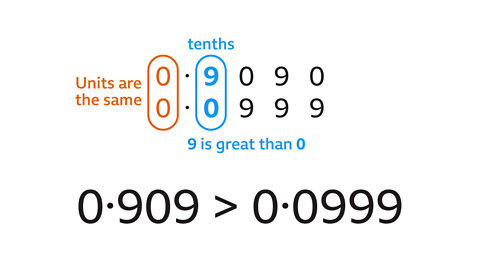
- List the numbers one on top of the other.
- Line up the decimal points.
- Compare digits one column at a time working left to right.
- This can be written as an inequality 0·909 > 0·0999.
How to add and subtract decimal numbers
Follow the examples and working out below:
- Write the numbers in a list, one on top of the other, lining up the decimal points.
- For subtraction the larger value is written above the smaller number.
- Write a decimal point, lined up, in the answer space.
- Use the same method as for whole numbers.
GCSE exam-style questions
- Work out the total of 7 + 29∙9 + 0∙23.
The total is 37·13.
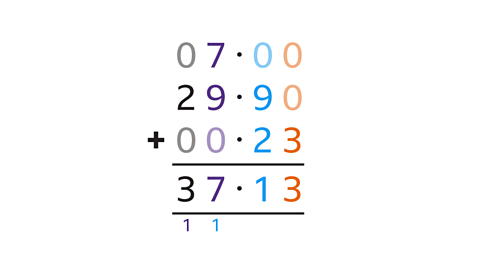
- List the numbers, lining up the decimal points.
- Write a decimal point, lined up, in the answer space.
- Insert extra zeros so that each number has the same number of digits.
- Add up using column addition:
- 7 + 29∙9 + 0∙23 = 37·13
- Add 0·3 and 5.
The total is 5·3.
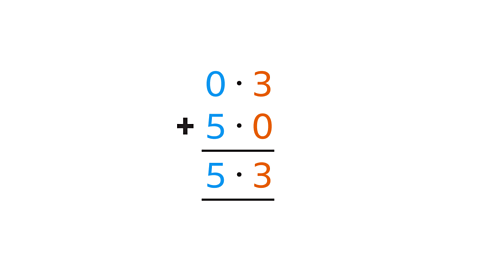
- List the numbers vertically, lining up the decimal points.
- The decimal point for a whole number comes after the units digit.
- Write a decimal point in the answer space.
- Add using column addition:
- 0·3 + 5 = 5·3
How to multiply decimal numbers
Follow the examples and working out below:
- Write each number as a whole number.
- Multiply the whole numbers.
- Place the decimal point in the correct position in the answer.
GCSE exam-style questions
- Work out 0·7 × 0·1 × 0·3.
The product is 0·021.
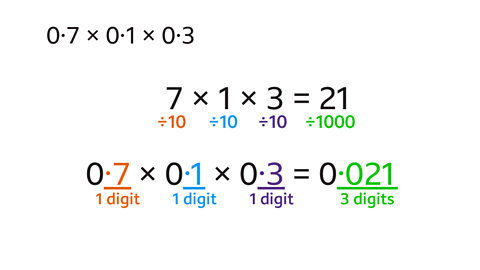
- Write each decimal number as a whole number:
7 × 1 × 3 = 21. - Each of the original numbers is a whole number, divided by 10, and has one digit after the decimal point.
- The answer needs to be divided by 1000
(10 × 10 × 10) to have three digits after the decimal point:
21 ÷ 1000 = 0·021.- So, 0·7 × 0·1 × 0·3 = 0·021.
- Work out 0·37 × 0·04.
The product is 0·0148.

- Write each decimal number as a whole number:
37 × 4 = 148.- 0·37 has two digits after the decimal point
(37 ÷ 100). - 0·04 has two digits after the decimal point
(4 ÷ 100).
- 0·37 has two digits after the decimal point
- The answer needs to be divided by 10,000
(÷ 100 ÷ 100) to have four digits after the decimal point:
148 ÷ 10000 = 0·0148.- So, 0·37 × 0·04 = 0·0148.
How to divide decimal numbers
Dividing decimals by whole numbers works in the same way as dividing whole numbers, where it’s important to make sure the decimal points are lined up.
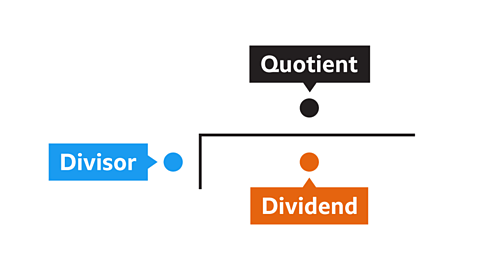
In the bus stop method:
- The divisorThe number by which another is divided, eg in the calculation 30 ÷ 6 , the divisor is 6. goes outside the bus stop.
- The dividendIn division, the number that is divided, eg in the calculation 30 ÷ 6, 30 is the dividend. goes inside the bus stop.
- The quotientThe result of a division, eg in the calculation 30 ÷ 6 = 5, the quotient is 5. goes on top of the bus stop.

To divide by a decimal, use equivalent fractionA fraction with the same value as another. Each fraction represents the same proportion, eg ½ and ¹⁰⁄₂₀. to make the calculation a division by a whole number.
Follow the working out below
GCSE exam-style questions
- Work out 9·54 ÷ 0·003.
The answer (quotient) is 3180.
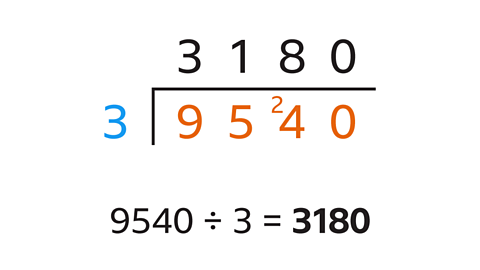
- Multiply both values by 1000, which gives an equivalent calculation.
- The calculation becomes 9540 ÷ 3.
- Write the division in bus stop form and work through the division from left to right.
- 9 ÷ 3 = 3
- 5 ÷ 3 = 1 remainder two.
- 4 becomes 24.
- 24 ÷ 3 = 8
- 0 ÷ 3 = 0, so 9·54 ÷ 0·003 = 3180.
Check your understanding
Quiz
Practise what you've learned about decimals with this quiz. The quiz questions change each time you try, so keep testing your knowledge.
Now that you've revised what decimal numbers are, why not look at how to convert recurring decimals?
More on Number
Find out more by working through a topic
- count5 of 15

- count6 of 15

- count7 of 15
