Key points about how to convert recurring decimals
- Understanding The agreed notation for repeated digits in a decimal, eg 0·75̇̇ = 0.755555… and 0∙29142914291421942194… = 0·2̇̇914̇̇. in A decimal with an infinitely repeating digit or block of digits, eg ⅓ is the decimal 0.3333…, also referred to as nought point three recurring or 0·3̇̇. A dot is written over the repeating digit or over the first and last of a group of repeating digits. is essential to writing out long recurring numbers in shorthand form.
- A A decimal with an infinitely repeating digit or block of digits, eg ⅓ is the decimal 0.3333…, also referred to as nought point three recurring or 0·3̇̇. A dot is written over the repeating digit or over the first and last of a group of repeating digits. exists when digits repeat forever. It may be a single digit (0∙55555…) or a group of repeated digits (0∙2360360…).
- A recurring decimal may be converted to a fraction using an Using letters to represent variables and unknown numbers in methods involving algebra..
Support your knowledge with these guides on how to simplify fractions and what fractions are.
Video – Converting recurring decimals
Watch this video to find out how to convert recurring decimals into fractions.
Converting recurring decimals.
Higher tier.
These are decimal numbers, and dots above some of the digits make them recurring decimals.
One dot means the digit under it repeats infinitely. In other words, it goes on forever (and ever and ever).
Two dots next to each other mean both digits repeat infinitely, or recur, in the order in which they appear.
And two dots on non-consecutive digits means those digits, and all the digits between them, recur infinitely in the same order.
An important skill in Maths is converting recurring decimals into fractions. So, let's look at some examples:
Question 1 says: Write 0.4-recurring as a fraction.
The first step is always to assign an algebraic variable to represent the decimal you're converting. So, let x equal 0.4-recurring, or 0.4444, and so on.
The next step is to make another number with the exact same recurring digits, and you can do this by moving one repeating unit, which in this case is just 4, to the left of the decimal point. To do that, multiply both sides of the equation by 10.
Now write 'x equals 0.4 recurring' underneath and line up the decimal points.
Notice that everything after the decimal point is the same for both 10x and x.
This means that if we subtract these equations, everything after the decimal point will cancel out. In other words, subtracting x from 10x will cancel out the recurring digits.
10x subtract x equals 9x and 4 subtract 0 equals 4, so 9x equals 4.
Now divide both sides by 9 to get x equals 4 over 9.
But remember, x equals 0.4-recurring. So, 0.4-recurring written as a fraction is four ninths.
Next question:
Write 1.352-recurring as a fraction.
This is a little more complicated, but the same method can be used.
Pause the video and have a go.
First, let x equal 1.352 all recurring.
This time, you need to multiply by a number that moves the entire repeating unit, 352, to the left side of the decimal point.
Multiplying both sides of the equation by 1000 moves the digits three places to the left, giving 1000x equals 1352.352 recurring.
Then, write out 'x equals 1.352 recurring' beneath this, with the decimal points lined up.
This shows that everything after the decimal point is the same, for both 1000x and x.
So, subtract x from 1000x to cancel out the recurring digits, leaving whole numbers on the right-hand side of the equation.
1000x subtract x equals 999x, and 1352 subtract 1 equals 1351.
Then, dividing both sides by 999 tells you that 1.352 all recurring, equals 1351 over 999 as a fraction.
Check your understanding
How to use dot notation for recurring decimals
Understanding The agreed notation for repeated digits in a decimal, eg 0·75̇̇ = 0.755555… and 0∙29142914291421942194… = 0·2̇̇914̇̇. in A decimal with an infinitely repeating digit or block of digits, eg ⅓ is the decimal 0.3333…, also referred to as nought point three recurring or 0·3̇̇. A dot is written over the repeating digit or over the first and last of a group of repeating digits. is essential to writing out long recurring numbers in shorthand form.
- A dot over a single digit means that digit is repeated infinitely.
- 0∙555555… = \(0·\dot{5}\)
- Two dots over non-consecutive digits mean that those digits, and all the digits in between them, recur infinitely in the same order.
- 0∙2360360… = \(0·2\dot{3}6\dot{0}\)
Follow the working out below
GCSE exam-style questions
- Write these recurring decimals using dot notation:
a) 0∙2533333333…
b) 0∙2633633633…
c) 0∙2030505050…
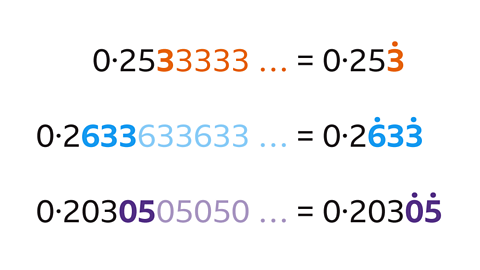
a) 0·2533333333 … = \(0{\cdot}25\dot{3}\)
- The decimal has a single digit repeat (3).
- Write the decimal with a dot over the first 3.
b) 0·2633633633 … = \(0{\cdot}2\dot{6}3\dot{3}\)
- The decimal has a block of three repeating digits (633).
- Write the decimal with a dot over the first digit and last digits of the repeating block.
c) 0·2030505050 … = \(0{\cdot}203\dot{0}\dot{5}\)
- The decimal has a block of two repeating digits (05).
- Write the decimal with a dot over the first digit and last digits of the repeating block.
- Write each decimal without dot notation:
a) \(0{\cdot}\dot{8}\)
b) \(0{\cdot}\dot{8}2\dot{5}\)
c) \(0{\cdot}004\dot{1}\)
a) \(0{\cdot}\dot{8}\) has a repeating single digit, eight (8), this gives 0·888888 …
b) \(0{\cdot}\dot{8}2\dot{5}\) has a repeating block of three digits (825), this gives 0·825825825 …
c) \(0{\cdot}004\dot{1}\) has a repeating single digit (1), this gives 0·00411111 …
How to convert recurring decimals
When converting a recurring decimal to a fraction, use the longer format of the number:
- Let the recurring decimal equal a A quantity that can take on a range of values, often represented by a letter, eg 𝑛, 𝑥, 𝑦, 𝑧, 𝑡 … etc. (𝑥).
- Count the number of digit(s) that repeat and multiply by the The power of ten tells us how many times to use the number in a multiplication. For example 10² means 10 × 10 = 100. Powers of ten are 10, 100, 1000 and so on. :
a. For one digit repeated, multiply by 10.
b. For two digits repeated, multiply by 100.
c. For three digits repeated, multiply by 1000, and so on. - Subtract the original decimal, to give 9𝑥, 99𝑥 or 999𝑥.
- Write 𝑥 as a fraction, multiplying by a power of ten if necessary, so that the Number written at the top of a fraction. The numerator is the number of parts used, eg for ⅓, the numerator is 1. and Number written on the bottom of a fraction. The denominator is the number of equal parts, eg for ⅓, the denominator is 3. are whole numbers.
- To reduce a fraction to its simplest form, also known as its lowest terms. the fraction if possible.
Follow the working out below
GCSE exam-style questions
- Write the recurring decimal \(0{\cdot}\dot{1}\dot{8}\) as a fraction.
\(0{\cdot}\dot{1}\dot{8}\) = \(\frac{2}{11}\)
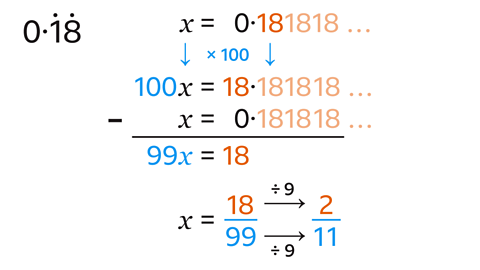
- Let 𝑥 be the recurring decimal.
- The decimal has a 2-digit repeat, so multiply by 100. This gives 100𝑥.
- Subtract the original decimal: 100𝑥 − 𝑥 = 99𝑥.
- Write 𝑥 as a fraction.
- Simplify the fraction by dividing by the numerator (18) and denominator (99) by their HCF (9).
- Prove algebraically that: \(0{\cdot}2\dot{3}\dot{6}\) = \(\frac{13}{55}\)
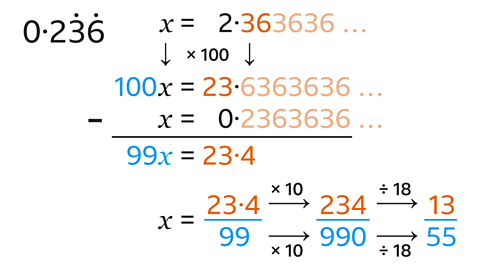
- Let 𝑥 = the decimal.
- The decimal has a 2-digit repeat, so multiply by 100.
- Subtract the original decimal.
- Write 𝑥 as a fraction.
- The numerator is not a whole number so multiply both the numerator (23·4) and the denominator (99) by 10.
- Simplify the fraction by dividing by the numerator (234) and denominator (990) by their HCF (18).
Now you've revised how to convert recurring decimals, why not look at negative and fractional indices?
More on Number
Find out more by working through a topic
- count6 of 15
- count7 of 15
- count8 of 15
