Key points about equations of parallel and perpendicular lines

parallelParallel lines are always the same distance apart. They never meet. lines have the same gradientA measure of the slope of a line..
Higher - perpendicularPerpendicular lines are at right angles to each other. lines have gradients that are the negative reciprocalWritten as 1 divided by the number, eg the reciprocal of 2 is ½ and the reciprocal of ½ is 2. The reciprocal is also called the multiplicative inverse. Any non-zero number multiplied by its reciprocal is equal to one. of each other.
Higher - The gradients of two perpendicular lines will always multiply to make –1.
Make sure you are familiar with finding the equation of a line and calculating gradient to understand equations of parallel lines.
If you are working at Higher tier, make sure you are confident with dividing fractions to work with gradients of perpendicular lines.
Equations of parallel lines
The equation of a straight line is 𝑦 = 𝑚𝑥 + 𝑐 where 𝑦 is the subjectThe subject of a formula or equation is the variable on its own on one side of the equals sign, eg 𝑦 is the subject in 𝑦 = 3𝑥 + 5. of the equation, 𝑚 is the gradientA measure of the slope of a line., and 𝑐 is the𝑦-interceptThe point at which the line crosses the 𝑦-axis..
Parallel lines never meet and are always the same distance apart. They have the same gradient.
Equations of parallel lines have the same value of 𝑚, the coefficientA number or symbol multiplied with a variable or an unknown quantity in an algebraic term. For example, 4 is the coefficient of 4n². of 𝑥. To compare the values of 𝑚, the equations may need to be rearranged so that 𝑦 is the subject.
For any given line, there are an infiniteUnlimited, goes on forever without end. Unable to be counted. An endless number. number of parallel lines with an endless number of 𝑦-intercepts.
To find the equation of a particular parallel line, substituteIn algebra, to replace a letter with a number. the 𝑥 and 𝑦-coordinates of a point on the line into the equation 𝑦 = 𝑚𝑥 + 𝑐. The specific 𝑦-intercept can then be found by solving for 𝑐.
Follow the working out below
GCSE exam-style questions

- Find the equation of the line parallel to 𝑦 = 5𝑥 + 7 that passes through (0, 4).
𝑦 = 5𝑥 + 4
The gradient of the line 𝑦 = 5𝑥 + 7 is the coefficient of 𝑥, which is 5.
Any parallel line must have the same gradient of 5.
The 𝑦-intercept is given in the coordinate (0, 4) as this is where the line crosses the 𝑦-axis. The 𝑦-intercept is 4.
Substitute the gradient and 𝑦-intercept into the equation 𝑦 = 𝑚𝑥 + 𝑐.
- Show clearly that the lines 𝑦 = 3𝑥 + 7 and 2𝑦 – 6𝑥 = 10 are parallel.
To show that two lines are parallel, they must have the same gradient. The gradient is the coefficient of 𝑥 when the equation is in the form 𝑦 = 𝑚𝑥 + 𝑐.

The first equation 𝑦 = 3𝑥 + 7 is in the required form, but the second equation, 2𝑦 – 6𝑥 = 10 needs to be rearranged.
Add 6𝑥 to both sides to give 2𝑦 = 6𝑥 + 10.
Divide both sides by 2 to give 𝑦 = 3𝑥 + 5.
It is now clear that the two lines both have a gradient of 3 so are therefore parallel.
- Find the equation of the line parallel to 𝑦 = 4𝑥 + 3 that passes through (–5, –2).
𝑦 = 4𝑥 + 18
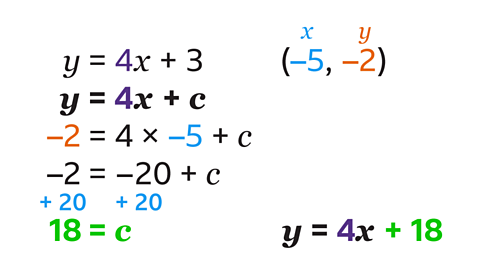
The gradient of the line 𝑦 = 4𝑥 + 3 is the coefficient of 𝑥, which is 4.
Any parallel line must have the same gradient of 4.
The equation of the parallel line must be of the following form:
𝑦 = 4𝑥 + 𝑐.Substitute the 𝑥-coordinate (–5) and 𝑦-coordinate (–2) into the equation.
Calculate the value of 4 × –5 and then solve the equation to find the value of 𝑐.
The 𝑦-intercept, 𝑐, is 18.
Quiz – Equations of parallel lines
Practise what you have learned about equations of parallel lines with this quiz.
Parallel and perpendicular lines – interactive activity
Use the interactive activity to see how lines are either parallel, perpendicular or neither, when selecting two graphs.
Equations of perpendicular lines are assessed at Higher tier only.
Check your understanding
Higher - Equations of perpendicular lines
Perpendicular lines are at right angles to each other.
If the gradientA measure of the slope of a line. of a line is 𝑚, the gradient of the perpendicular line is –\(\frac{1}{m} \). The gradients of the two lines are the negative reciprocalWritten as 1 divided by the number, eg the reciprocal of 2 is ½ and the reciprocal of ½ is 2. The reciprocal is also called the multiplicative inverse. Any non-zero number multiplied by its reciprocal is equal to one. of each other.
If the gradients of two perpendicular lines are multiplied, the result is –1.
Follow the working out below
GCSE exam-style questions

- What is the gradient of any line perpendicular to 𝑦 = 2 – \(\frac{1}{5} \) 𝑥 ?
5
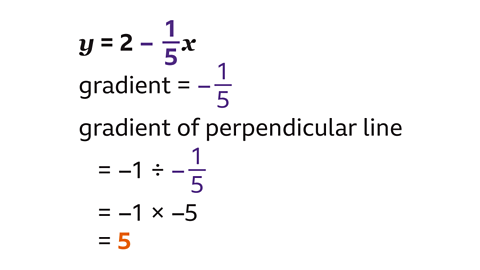
The gradient of the line 𝑦 = 2 – \(\frac{1}{5} \)𝑥 is the coefficient of 𝑥, – \(\frac{1}{5} \).
The gradient of a perpendicular line is the negative reciprocal of – \(\frac{1}{5} \).
The negative reciprocal of a number is –1 divided by the number.
–1 ÷ –\(\frac{1}{5} \) is the same as –1 × –5, which is 5.
- Show that the lines given by the equations 3𝑦 – 2𝑥 = 9 and 2𝑦 = –3𝑥 + 8 are perpendicular.
Neither equation is in the form 𝑦 = 𝑚𝑥 + 𝑐 to identify the gradient, 𝑚. They must be rearranged.
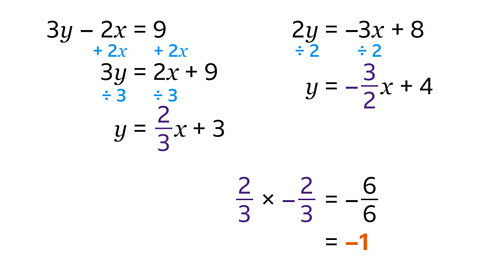
For the first equation, add 2𝑥 to both sides and divide both sides by 3. Make sure to divide each part of the right-hand side by 3. This gives 𝑦 = \(\frac{2}{3} \)𝑥 + 3.
For the second equation, divide both sides by 2. This gives 𝑦 = –\(\frac{3}{2} \)𝑥 + 4.
The gradient of the first equation is \(\frac{2}{3} \). The gradient of the second equation is –\(\frac{3}{2} \).
The two gradients are negative reciprocals of each other because they multiply to make –1. Therefore, the two lines are perpendicular.
- Find the equation of the line perpendicular to 𝑦 = –4𝑥 + 7 that passes through (12, 1)
𝒚 = \(\frac{1}{4} \)𝒙 – 2
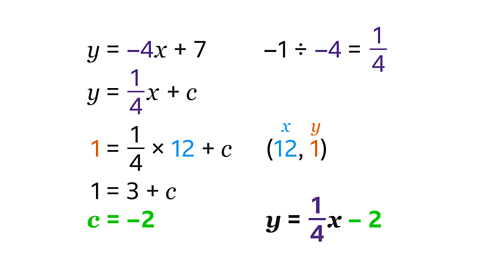
The gradient of the line 𝑦 = –4𝑥 + 7 is –4. The gradient of the perpendicular line is the negative reciprocal of –4, which is \(\frac{1}{4} \).
Substitute the 𝑥-coordinate (12) and 𝑦-coordinate (1) of the point into the equation in place of 𝑥 and 𝑦.
The value of \(\frac{1}{4} \) × 12 is 3. Solve the equation to find the value of 𝑐. The 𝑦-intercept, 𝑐, is –2.
Write the equation of the perpendicular line with its gradient of 1/4 and 𝑦-intercept of –2. The equation of the line is 𝑦 = \(\frac{1}{4} \)𝑥 – 2.
Video – Perpendicular lines
Use the equation 𝑦 = 𝑚𝑥 + 𝑐 to prove that perpendicular lines on a graph have negative reciprocal gradients. Watch the video to find out more.
Equations of perpendicular lines are assessed at Higher tier only.
Perpendicular lines.
What do you notice about the gradients of these two perpendicular lines, one half and –2?
Each is the negative reciprocal of the other. Remember, the reciprocal of a fraction is that same fraction, but with the numerator and denominator swapped.
And to find the reciprocal of a whole number, you can write it as a fraction with denominator 1 before flipping.
So, the negative reciprocal of one half is –2 over 1, or just –2, and the negative reciprocal of –2 is found by changing the sign, giving a positive value, and finding the reciprocal, one half.
The gradients of two perpendicular lines are always negative reciprocals of each other.
For example, the perpendicular gradient to 1 over 8 would be –8, and the perpendicular gradient to –5 over 4 would be 4 over 5.
This also means the gradients of perpendicular lines always multiply to give –1.
You can use these facts to answer questions about perpendicular gradients, even when there's no graph.
Let's look at an example question.
Which of these lines is perpendicular to 𝑦 equals 3𝑥 add 4: 2𝑦 equals 4𝑥 subtract 3, –3𝑥 add 𝑦 equals 3, or 3𝑦 equals 12 subtract 𝑥?
To find this out, we need to find the gradient of each line.
Remember that 𝑦 equals 𝑚𝑥 add 𝑐 represents the general equation of a straight line. When written in this form, with 𝑦 as the subject, the coefficient of 𝑥, m, is the gradient of the straight line.
So, the gradient of 𝑦 equals 3𝑥 add 4 is 3.
Then to solve the question, we need to make 𝑦 the subject of each equation, and then use the 𝑥 coefficient to determine the gradient. For 2𝑦 equals 4𝑥 subtract 3, dividing both sides by 2 gives 𝑦 equals 2𝑥 subtract 3 over 2.
This is now in the form 𝑦 equals 𝑚𝑥 add 𝑐, and so the gradient is 2.
For –3𝑥 add 𝑦 equals 3, adding 3𝑥 to both sides gives 𝑦 equals 3𝑥 add 3, showing that the gradient is 3. This is the same as the gradient of 𝑦 equals 3𝑥 add 4, meaning these two lines are actually parallel.
And for 3𝑦 equals 12 subtract 𝑥, dividing by 3 and then rearranging shows the gradient is –1 over 3. Negative one third and 3 are negative reciprocals of each other, so this means that 3𝑦 equals 12 subtract 𝑥 is perpendicular to 𝑦 equals 3𝑥 add 4. +
Higher – Quiz – Equations of parallel and perpendicular lines
Practise what you have learned about equations of parallel and perpendicular lines with this quiz for Higher tier.
Now that you have revised equations of parallel and perpendicular lines, why not try looking at equations of a line and calculating gradient?
More on Algebra
Find out more by working through a topic
- count2 of 14

- count3 of 14
- count4 of 14
