Challenge 4 - Test Scores
Challenge 4 is all about working out averages.
Maths teacher Chris Smith and pupils from Grange Academy are here to explain.
The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.
Teacher: This problem is all about averages. Mairi is about to take the last of a series of tests.
If she gets 23 in this test, it will improve her average by 1. If she scores 39 that will improve her average by 3.
What was Mairi's average score before the last test? Explain your answer.
Pupil: Try to think between the differences in the scores and what they can tell us.
Teacher: So what am I talking about here when I say average?
Pupil: So average is another word for the mean, which is basically if you add them all up and divide them by how many there are.
Pupil: You don't need to number the tests, but it may help.
Teacher: Add up all your test scores or Mairi's test scores and divide by how many schools she does.
But why is that a problem in this question?
Pupil: We don't know how many tests there were and we don't know the scores.
Pupil: You could use algebra to make two equations that you can compare.
Pupil: Go for it.
So here's the challenge:
Mairi is about to take the last of a series of tests.
If she gets 23 in this test, it will improve her average by 1.
If she scores 39, it will improve her average by 3.
What was Mairi’s average score before the last test?

Need a hint?
- Think about the differences between the scores, what that can tell us?
- You don’t need to know the number of tests but it might help
- Could you use algebra to make two equations that you can compare?
Solution
Worked out the answer? Here's how you can do it.
Did you work out what Mairi's previous test score average was? Let's look at how we got our answer.
We know that a score of 23 will improve Mairi's average by one, and a score of 39 will improve her average by three.
We can subtract and compare the difference. 39 subtract 23 is 16. 3, subtract 1 is 2.
So 16 marks increases the average by two. This means that 8 marks increases the average by 1.
Remember that a score of 23 will also increase the average by 1.
So if we subtract 8 from 23, we will get back to the average 23.
Subtract 8 is 15 which was the previous average.
Great job if you aced that test.

Step 1
We know that a score of 23 will improve Mairi's average by 1.
And a score of 39 will improve her average by 3.
We can subtract and compare the difference.


Step 2
39 - 23 = 16
3 - 1 = 2
So 16 marks increases the average by 2.

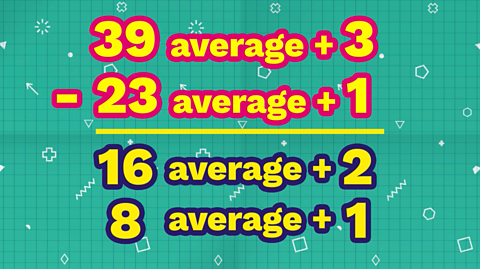
Step 3
This means 8 marks increases the average by 1.
Remember that a score of 23 will also increase the average by 1.
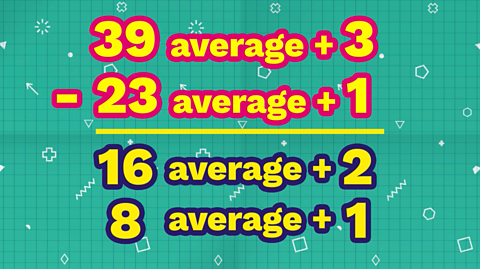

Step 4
So if we subtract 8 from 23, we will get back to the average.
23 - 8 = 15
So Mari's previous average score was 15.

Solution using algebra
Another way to solve this is by using algebra.
If Mairi has to sit \(n\) tests overall, then she has currently completed \(n - 1\) tests.
The symbol for a common average is \(\bar{x}\), so Mairi's current total score is \((n - 1)\bar{x}\).
If Mairi sits the final test and scores \(23\), we can write this by adding \(23\) to the expression:
\((n-1)\bar{x}+23\)
We also know that this increases her average by one. We can write this as:
\(n(\bar{x}+1)\)
Turn this into an equation:
\(n(\bar{x}+1)=(n-1)\bar{x}+23\)
Simplify:
\(n\bar{x}+n=n\bar{x}-\bar{x}+23\)
\(n=-\bar{x}+23\)
Rearrange:
\(n+\bar{x}=23\)
If Mairi sits the final test and scores \(39\), we can write this as:
\((n-1)\bar{x}+39\)
We also know that this increases her average by three. We can write this as:
\(n(\bar{x}+3)\)
Turn this into an equation:
\(n(\bar{x}+3)=(n-1)\bar{x}+23\)
Simplify:
\(n\bar{x}+3n=n\bar{x}-\bar{x}+39\)
\(3n=-\bar{x}+39\)
Rearrange:
\(3n+\bar{x}=39\)
We can subtract one of these equations from the other to find the value of \(n\):
\(3n+\bar{x}-(n+\bar{x})=39-23\)
\(2n=16\)
\(n=8\)
We can now put the value of \(n\) into one of the equations to find the value of \(\bar{x}\).
\(n+\bar{x}=23\)
\(15+\bar{x}=23\)
\(\bar{x}=8\)
So Mairi sits eight tests overall. She has already sat seven tests and her current average score is 15.
Maths Week Scotland 2023. listMaths Week Scotland 2023
Try out all the daily challenges from Maths Week Scotland 2023.

Maths Week Scotland 2022. listMaths Week Scotland 2022
Try out all the daily challenges from Maths Week Scotland 2022.

Maths Week Scotland 2021. listMaths Week Scotland 2021
Want more maths challenges? Here are all the problems from 2021.

More on Maths Week Scotland 2024
Find out more by working through a topic
- count1 of 8
