Key points about inequalities

Algebraic inequality (algebra)A relationship between two expressions or values that are not equal to each other. such as 𝑛 < 5 and 4 ≤ 𝑛 < 7 can be represented on a number line using circles, arrows and lines.
Inequalities are solved in a similar way to solving equations, using inverse operationThe opposite of a mathematical process. For example, the inverse of × 5 is ÷ 5. The inverse operation undoes the original process. .
integerIntegers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, –8, and 10,000 are examples of integers. solutions are a set of numbers that satisfyWhen a value makes an equation, inequality or statement true. an inequality.
Refresh your knowledge of this topic with this guide on solving equations.
Video – Solving inequalities
Watch this video to learn about inequalities and how to represent them using number lines.
Solving inequalities.
In some real-world situations, values like your age or height must be within a given range of numbers.
Let's look at how to use inequality symbols to represent a set of values. First, you need a variable, which is a letter that can take a range of values.
Let's say 𝑆 represents the score in a video game. The rule in the game is that you must score more than 8 to advance to the next level. This means your score, 𝑆, must be greater than 8.
Remember, the smaller pointed end of the inequality symbol always points to the smaller of the two values.
Here, 𝑆 must be greater than 8, so 8 is the smaller value, and the big gap points to the larger of the two values, which in this case is 𝑆.
How about a travelcard for people between and including the age of 16 and 25? A person's age, 𝐴, must be greater than or equal to 16, and it must be less than or equal to 25.
Notice that the inequality symbols have horizontal lines underneath. This indicates that 𝐴 can equal 16 or 25, as well as all the values in between.
And how might we show a cinema ticket discount available to under 18s, as well as those who are 65 or over? This needs two inequalities. A person's age, 𝐴, must be less than 18 or greater than or equal to 65 to qualify for the discount.
We can also represent the solutions to inequalities on number lines.
For ‘𝑆 is greater than 8’, draw a circle at 8 and then a horizontal arrow stretching to the edge of the number line in the direction of the larger values. The arrowhead shows that this continues forever. This inequality is true for all numbers larger than 8. The circle should be empty to show that 8 itself is not a solution.
To check the arrow is on the correct side of the circle, we can check a value either side of the circle. 13 is greater than 8, which means it's a valid solution, while 6 is not greater than 8, so the arrow is on the correct side.
For ‘𝐴 must be between 16 and 25’, draw filled circles at 16 and 25, and then a horizontal line between them to represent the possible solutions to the inequality. Notice the circles are filled because the values 16 and 25 are included in the solution.
And finally, if ‘𝐴 must be less than 18 or greater than or equal to 65’, you can show both inequalities on the same number line.
First, draw two circles at 18 and 65. But be careful! 𝐴 must be less than 18, which means the circle at 18 needs to be empty, but the 65 circle is filled because 65 is included. A horizontal arrow to the left represents values under 18 and an arrow to the right represents values over 65, so none of the values between the circles solve either inequality.
Check your understanding
Inequalities on a number line
Inequalities are used when values are not equal. Inequality signs compare the size of two values.
In algebra, inequalities are used to compare a variableA quantity that can take on a range of values, often represented by a letter, eg 𝑛, 𝑥, 𝑦, 𝑧, 𝑡 … etc. , (usually 𝑛 or 𝑥), with numbers. The inequality 𝑛 < 5 means 𝑛 is less than 5, which can also be read in reverse as 5 is greater than 𝑛.
Sometimes two inequalities can be combined. For example, 𝑛 > 3 and 𝑛 ≤ 7 can form 3 < 𝑛 ≤ 7.
Inequalities are represented on a number line with circles, lines and arrows. A circle represents the value (or values) 𝑛 is being compared with. The circle is shaded or unshaded depending on whether 𝑛 can equal that value or not.
Follow the working out below
GCSE exam-style questions

- Write the inequality for 𝑛 shown by the number line.
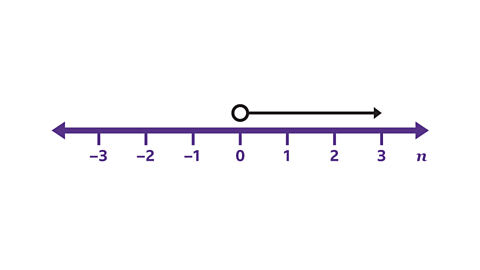
𝒏 > 0
The arrow represents the values greater than 0. The circle at 0 is not shaded, so 𝑛 cannot equal 0. 𝑛 is greater than 0.
- Write the inequality for 𝑛 shown by the number line.
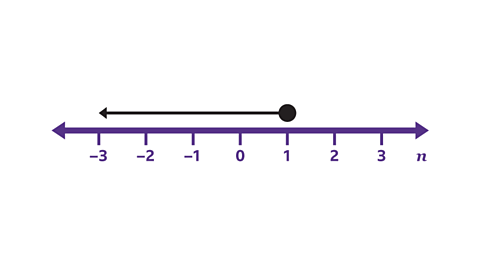
𝒏 ≤ 1.
The arrow represents the values less than 1. The circle at 1 is shaded, so 𝑛 can equal 1. 𝑛 is less than or equal to 1.
- Write the inequality for 𝑛 shown by the number line.
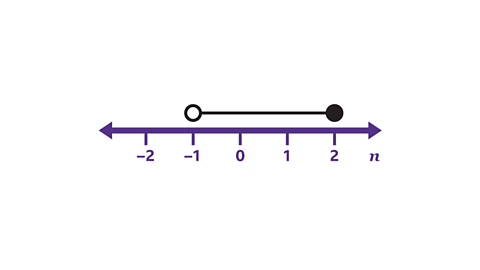
–1 < 𝒏 ≤ 2
The circle at –1 is not shaded, so 𝑛 cannot equal –1.
The circle at 2 is shaded so 𝑛 can equal 2.
The line between the two values shows 𝑛 can be between –1 and 2.
𝒏 is greater than –1. 𝑛 > –1, or in reverse, –1 < 𝑛.
𝒏 is less than or equal to 2. 𝑛 ≤ 2.
Put these inequalities together to form –1 < 𝑛 ≤ 2.
How to solve inequalities
Inequalities are solved by performing inverse operationThe opposite of a mathematical process. For example, the inverse of × 5 is ÷ 5. The inverse operation undoes the original process. to isolate the variable, similar to solving equations.
If both sides of an inequality are multiplied or divided by a negative number, the sign must be reversed, i.e. from > to <.
If an inequality has three parts, such as 14 < 3𝑛 – 1 < 20, operations need to be applied to all three parts.
Follow the working out below
GCSE exam-style questions
- Solve 2 − 5𝑛 ≤ 32.
𝒏 ≥ − 6
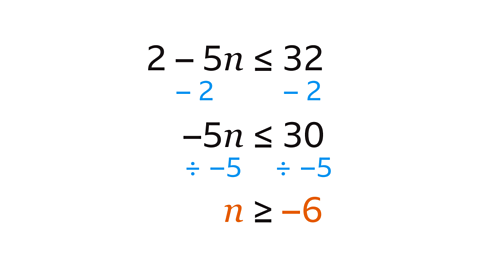
𝑛 has been multiplied by − 5 and then 2 is added.
Perform inverse operations to both sides of the inequality.
Subtract 2 from both sides to give −5𝑛 ≤ 30. Remember to keep the negative sign with the 𝑛 term.
Divide both sides by −5 to give 𝑛 ≥ − 6. When both sides of an inequality are multiplied or divided by a negative number, the inequality sign is reversed.
- Solve 18 < 7𝑛 − 10 ≤ 25.
4 < 𝒏 ≤ 5
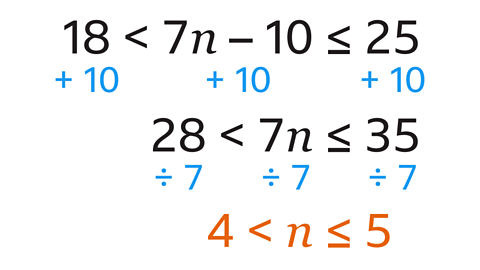
𝑛 has been multiplied by 7 and then 10 is subtracted.
Perform inverse operations on all three parts of the inequality.
Add 10 to each part to give 28 < 7𝑛 ≤ 35.
Divide each part by 7 to give 4 < 𝑛 ≤ 5.
How to find integer solutions to inequalities
For an inequality for 𝑛, there is an infiniteUnlimited, goes on forever without end. Unable to be counted. An endless number. amount of values that 𝑛 can take. For example, if 𝑛 > 4, then 𝑛 could be any number greater than 4, including decimals, such as 4·0001 or 11·2.
The infinite number of values for 𝑛 can be reduced by listing a set of integer solutions. An integer is a number that does not have a decimal or fraction part, eg −4, 0, or 37.
A solution set is a set of values that make the inequality true. These values are said to satisfyWhen a value makes an equation, inequality or statement true. the inequality.

Did you know?
The set of whole numbers is made up of zero and positive numbers with no decimal part (0, 1, 2, 3, …).
The set of integers is made up of all the whole numbers and negative numbers with no decimal part
(…−3, −2, −1, 0, 1, 2, 3, …).
Follow the working out below
GCSE exam-style questions

- Write down all the integers that satisfy –3 < 𝑛 ≤ 2.
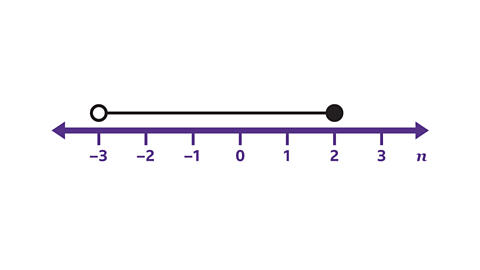
2, −1, 0, 1 or 2
The inequality states that 𝑛 can take any value between −3 and 2. 𝑛 cannot equal −3, but it can equal 2.
An integer is a number that does not have a decimal part. The integers that satisfy the inequality are −2, −1, 0, 1 or 2.
- What is the largest integer that satisfies the inequality 2𝑛 < 7?
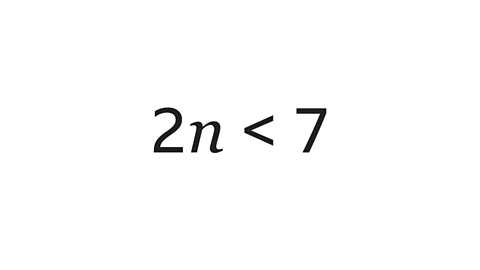
3
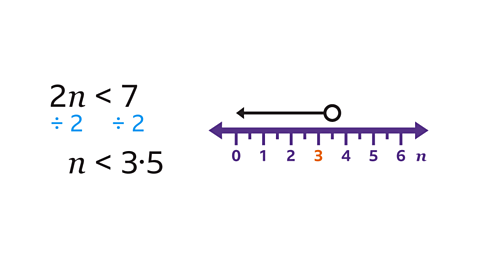
Solve the inequality so that 𝑛 is on its own. Divide both sides by 2 to give 𝑛 < 3.5.
An integer does not contain a decimal part. 𝑛 must be less than 3.5. The largest integer less than 3.5 is 3.
- List the integers that satisfy both inequalities represented on the number line.
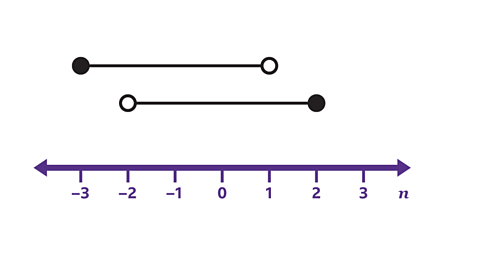
–1 and 0
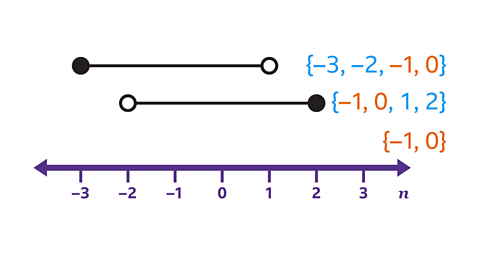
The first inequality contains values of 𝑛 greater than or equal to –3 but less than 1. 𝑛 cannot equal 1. The set of possible integers is {–3, –2, –1, 0}.
The second inequality contains values of 𝑛 greater than –2 and less than or equal to 2. 𝑛 cannot equal –2. The set of possible integers is {–1, 0, 1, 2}.
The integers that satisfy both inequalities are the numbers in both sets.
Quiz – Inequalities
Practise what you've learned about inequalities with this quiz.
Now that you have revised inequalities, why not try looking at geometric and special sequences?
More on Algebra
Find out more by working through a topic
- count9 of 14
- count10 of 14

- count11 of 14
- count12 of 14